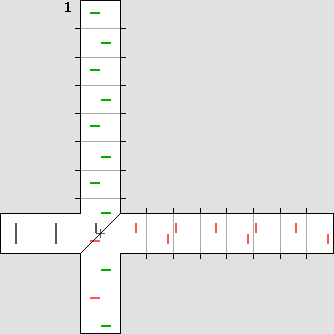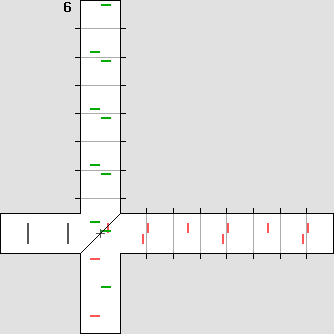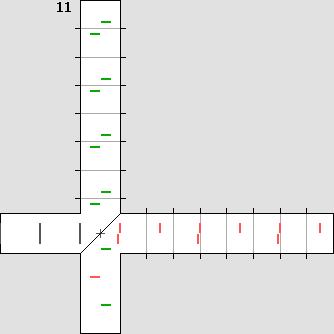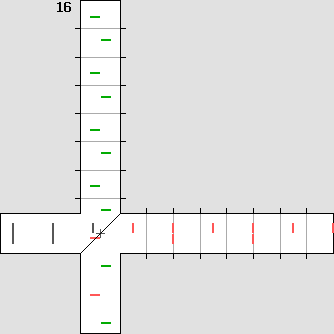
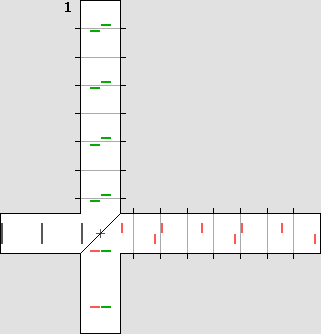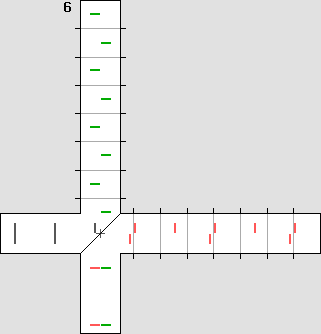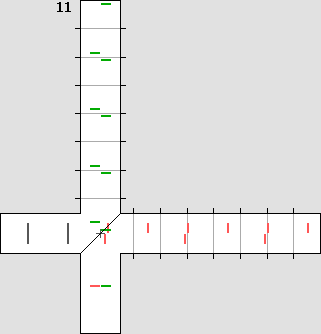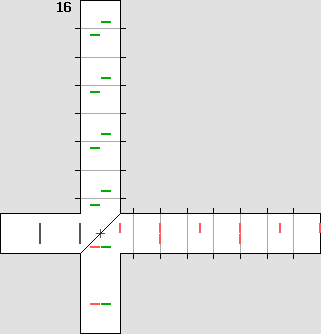
Michelson's plan was to detect the phase shift shown on the left.
However, Lorentz was right: there is no phase shift because the interferometer contracts.
A GREAT IDEA
|
In 1887, Albert A. Michelson tried to detect the speed of the Earth through aether by means of an interferometer. But his apparatus revealed nothing. It was a "failure". Actually, this experiment led to a fantastic scientific discovery: the Lorentz transformations and the theory of Relativity. A race between two planes. Michelson explained to his children that his interferometer was simulating a race on a river between two swimmers. In 1887 planes did not exist. Otherwise, he certainly would have spoken about a plane race while a strong wind is blowing. Let us consider two identical airplanes which constant speed is 100 mph. Suppose the wind blows at 50 mph. The beta normalized speed is given by v / c = 50 / 100 = .5. According to the rules, both pilots must perform a round trip between two points 100 miles apart. The first pilot prefers to fly in the direction of the wind. The second one chooses the transverse route, and he easily wins the race. Those planes behave exactly like light waves. Their speed may be compared to the speed of light and one may consider that there is an aether wind. |
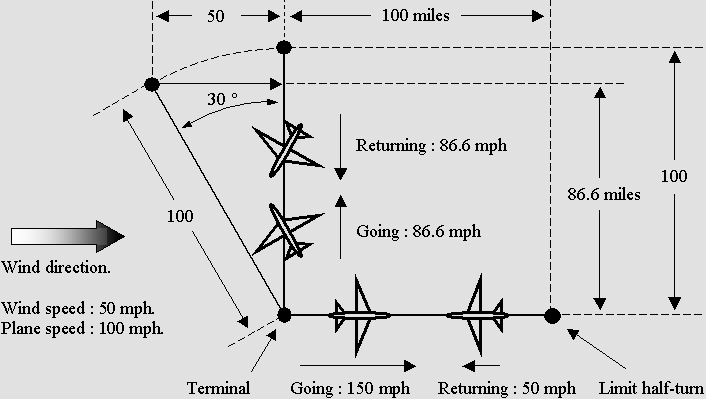
The Michelson interferometer works like a race between two planes.
|
Let's make it simple. The relative speed on a go and return trip is given by Lorentz's g contraction factor, which is the reciprocal of the gamma factor. In this example, beta = .5 and g = .866:
Then the relative speed on a round trip will be : Along the wind : g2 c g2 = .75 c 75 mph Across the wind : g c g = .866 c 86.6 mph Across the wind, the planes (or waves) will be tilted to 30° according to the theta angle: theta = arc sin beta In the absence of wind, the round trip would last 2 hours whatever the direction. However, in the presence of wind, the duration increases more severely in the direction of the wind according to g squared instead of g not squared in the transverse direction. 1 - The round-trip duration along the wind: 2 hours / g2 = 2.6667 hours. 2 - The round-trip duration across the wind : 2 hours / g = 2.3094 hours. So the plane flying across the wind will be: .357 hour = 21 minutes faster and the plane flying along the wind will be defeated. However, George F. FitzGerald and Hendrick Lorentz noted after Michelson's experiment that a shorter circuit on the displacement axis would cancel the difference. The interferometer would be contracted in accordance with Lorentz's g contraction factor. This is called the Lorentz transformations:
Lorentz's original equations using beta and g. The Michelson transformations. Prior to the Lorentz transformations, Michelson discovered a mechanical property of waves propagating in a moving frame of reference. This could be called the Michelson transformations, but it is more simply the regular Doppler effect. A wavelength contraction according to g occurs on both transverse y and z axes, but a more severe one according to g squared can be observed along the motion x axis. x' = (x – beta * t) / g 2 y' = y / g z' = z / g t' = t + beta * x According to our example, planes flying inside such an x, y and z contracted space would always perform the round trip in two hours whatever the speed of the wind or its direction. This explains why no abnormal time effect occurs. So the main difference between Michelson's transformation and Lorentz's is the time effect. Both should yield a null result for the interferometer. Galileo's transformation. Galileo's transformation also involves a t' – t duration according to beta * x, albeit all authors still put down t' = t. x' = x + beta * t y' = y z' = z t' = t + beta * x There is no transverse contraction. Please note that beta * t simply indicates a regular translation motion along a straight line. The plus sign is needed in order to indicate the correct position in the Cartesian frame of reference after a given t time because the rightward motion is a well admitted convention. However, from the moving observer's point of view, the x' equation can be reversed in an abnormal way: x' = x – beta * t. This procedure creates a different Galilean frame of reference, which is not Cartesian any more because it is moving. According to Descartes, the light propagates by means of the aether, which is postulated to be at rest. So the aether is a preferred frame of reference, also the only admissible Cartesian frame of reference. One should bear in mind that Galileo's transformation is wrong because matter actually transforms according to the Lorentz transformations. Matter especially cannot reach the speed of light. A race between two waves. Michelson discovered that the relative speed of light is slower in the direction of motion. He deduced from this that an interferometer could detect the speed of the aether wind. He understood that two orthogonal light beams would not produce the same interference fringes after a 90° rotation. Here is a diagram showing Michelson's apparatus:
|
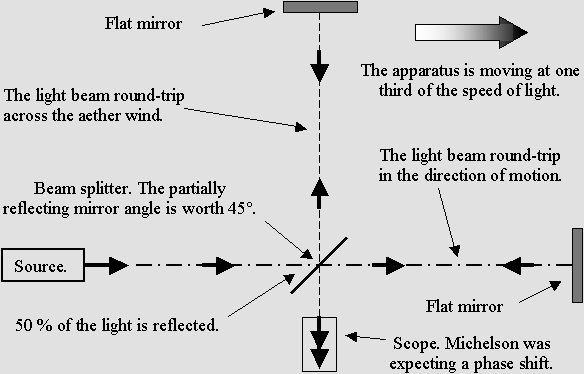
The Michelson interferometer.
|
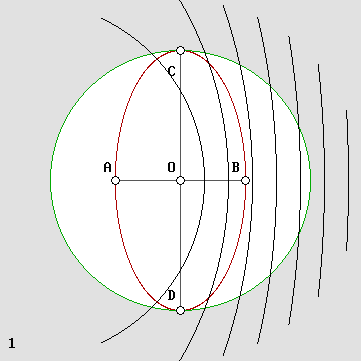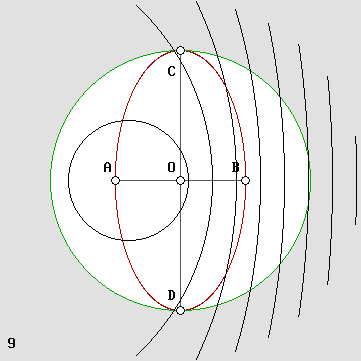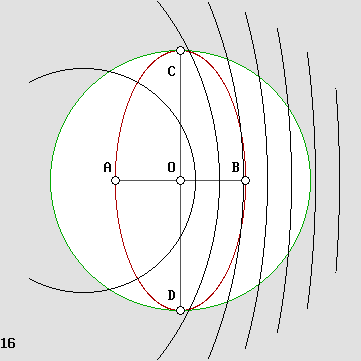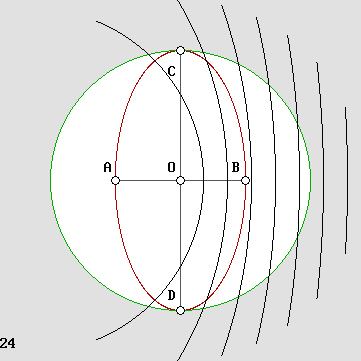
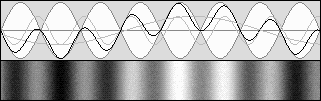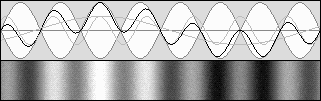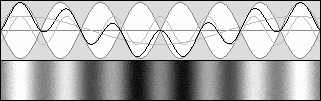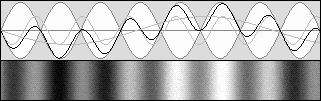
The light beam emitted by the source is separated into two halves by means of a beam splitter containing a 45° partially reflecting mirror. Then the beams are reflected on a flat mirror back to the beam splitter, which then reunifies them. Finally, both beams could be compared in a special scope. Michelson was expecting a phase shift. Waves would add themselves constructively or destructively, showing a characteristic interference pattern. The goal was to measure the fringes displacement after a 90° rotation. Such a rotation could be performed easily without any stress because the instrument was mounted on a large stone floating on a mercury pond. The temperature was also severely controlled. The Michelson interferometer animated diagrams. The animations below show what is going on inside the interferometer branches. In order to obtain a phase shift which is clearly visible, one must use a very high speed. Here, the interferometer speed is one third of the speed of light. Then beta = .3333 and g = .9428. Such a speed produces a 2 : 1 wavelength ratio R along the displacement axis, according to: R = (1 + beta) / (1 – beta) This ratio indicates that on-axis planes crossing the starting point each minute and one at a time would be two times nearer while flying against the wind. So one can imagine that each small red or green line shown below represents a plane. The aether wind blows from the right. Moreover, on the transverse axis, waves are compressed according to Lorentz' g contraction factor, .9428 here: lambda' = g * lambda The diagram on the left displays exactly the same length for both branches. This distance was calculated to obtain a full lambda / 2 phase shift. The wave fronts (or planes) along the motion axis are pictured in red and they are green crosswise. Michelson was expecting the phase shift shown on the left: |


|
The diagram on the right shows what really occurred, against Michelson's expectations. One of the branches (the horizontal one here) underwent a contraction according to Lorentz's g contraction factor. In this example, it contracts to 94.28 % of its original length. The waves' speed difference was cancelled and the wave fronts were still perfectly in phase after a 90° rotation. This explains why the Michelson interferometer cannot reveal the aether wind.
A new fact in science history: STANDING WAVE CONTRACTION
This web site shows that aether exists and that matter is made purely out of spherical standing waves. Because moving standing waves undergo a contraction, moving matter should also undergo a contraction. Lorentz was unaware of this. It is a new fact. Now one can explain why the Michelson interferometer contracts. Michelson and Lorentz strongly believed that aether should exist. So this page certainly matches their thoughts. However, this is not what scientists believe today, because they have wrongly ruled out aether.So this page does not submit to standard opinion, albeit it is consistent with Lorentz's 1904 book. The science world is rapidly evolving today because of the Internet. People familiar with Lorentz's researches generally admit a privileged frame of reference, which in most cases coincides with aether. Some of them prefer the word "space", but this is obviously a compromise because aether has become a suspicious subject nowadays. Such people can speak about Relativity. Others who did not read Lorentz's 1904 book should be less affirmative because they ignore how Relativity was discovered. Lorentz's was right. Most web pages on the Michelson interferometer explain that the null result showed that aether does not exist. This is totally false. Lorentz explained that the interferometer would undergo a contraction in the direction of motion. The first of Lorentz's three transformations is a length contraction, which occurs only on the x axis. For example, let us suppose a very high speed: 86.6% of the speed of light. Then beta = .866 and Lorentz's contraction factor is .5. The gamma factor equals the reciprocal: 1 / g = 2. The following animated diagram shows that the round-trip duration along any of the 4 possible paths inside the interferometer's arms would be the same. This device can be seen as a 4 branch interferometer. Here, the very high speed involves a severe contraction to half of the original length, and the speed difference becomes clearly visible: |
|
|
The contraction cancels the relative speed difference.
The Doppler effect.
|
For the same reason, any observer placed in the system's center O and using a radar signal would find by timing the echoes that all A, B, C and D distances are the same. However, he would not notice that the four radar echoes are two times longer because his clock also runs two times slower according to the gamma factor. Because all forces are transmitted by means of waves, which undergo the Doppler effect, all matter mechanisms are also slowed down in the same way. All happens with a slower rate of time. Most often, one speaks about time dilation. This is incorrect. Time is a concept, an idea; it does not really exist. A clock does exist, and it can tick slower. This does not mean that time runs slower. Secondly, waves (or planes) would reach the A point in the rear much more rapidly. Because of the Doppler effect, the B point will be attained later. Henri Poincare showed how, inside such a system, the central O observer must use light or radio signals in order to synchronize A and B clocks. Because the signal speed is much faster backward, A will be in advance and B will be late. However, nobody would be able to notice the resulting time shift. Inside such a moving frame of reference, Poincare showed that such local hours lead to a sort of virtual simultaneity. One cannot detect his actual speed any more. All happens as if the system was perfectly at rest inside aether. In addition, waves propagating forward contract according to 1 – beta while those moving backward expand according to 1 + beta. The backward wavelength expansion ranges only from 1 to 2 while waves can be infinitely compressed forward. It turns out that the wave compression is much more severe; it increases matter's energy according to the gamma factor. So matter's mass/energy is doubled for .866 c and this was also discovered by Lorentz. As a matter of fact, this phenomenon could be regarded as Lorentz's fourth transformation:1 – Distances along the displacement axis contract. 2 – All phenomena occur with a slower rate of time. 3 – A time shift appears between the front and the rear. 4 – Matter is gaining in mass and the mass gain becomes kinetic energy. This was the secret: matter is made of waves. 100 years were needed to solve this mystery. It was obvious, though, because Lorentz's equations are almost a copy of the Woldemar Voigt's ones on the Doppler effect (1887). Actually, the only difference was an unknown constant whose k = 1 value was finally discovered by Lorentz and Poincaré in 1904. It is that simple: matter behaves like waves. Standing wave contraction. Very few people noticed that because light waves are reflected back on the interferometer's mirrors, standing waves appear inside both of its branches. Moreover, in 1904, standing waves compression was not a well known phenomenon. As far as I know it has been discovered by Mr. Yuri Ivanov, and only me and Mr. Serge Cabala seem to have studied it in an acceptable manner. For more details about moving standing waves (Ivanov's "lively standing waves") see standing waves. So, in the animation, I managed to add some reference marks along both branches in order to locate the nodes' position. It should be pointed out that such nodes are still present in the direction of motion, notwithstanding the fact that the wavelength is two times longer while the waves are traveling backward. This is possible because those waves also seem to travel two times faster. One needs a little concentration to observe this, but it finally becomes obvious. The mean relative velocity of light in order to perform a complete round-trip can be calculated as shown above. Let's repeat that waves behave in exactly the same manner as planes in the presence of wind. So the compression rate is also given by g and g squared: Relative on-axis mean wave velocity: v = c g 2 On-axis standing wave compression: lambda' = lambda * g 2 Relative transverse constant wave velocity: v = c g Transverse standing wave compression: lambda' = lambda * g
Those results can also be established according to the "relative" Doppler effect. I elaborated the first equation below around 1998. It derives from the regular Doppler effect 1 – beta * cos phi, but the number one gradually transforms to g until phi reaches 90°. The second formula yields the same results; I adapted it from Mr. Ivanov's web site.
It should be pointed out that these equations also indicate the relative wave velocity according to Michelson's calculus. Using a 90° phi angle, one can easily note that transverse waves undergo a compression according to Lorentz's g factor. Because the relative transverse wave velocity is slowed down according to g, the time needed to perform the transverse go and return trip is also longer according to 1/g. The calculus for the on-axis whole round trip is a bit more complicated because the go and return trips are different, but one can use the simpler 1 – beta formula forward and 1 + beta backward. Finally, the standing wave compression ratio equals the change in the relative velocity of light on a go and return trip. Both calculi yield the same results. Michelson preferred velocity and did not use the standing wave method, which is simpler though, especially for studying the Kennedy-Thorndyke experiment. Actually, Kennedy and Thorndyke did not take the frequency reduction into account. The overall increased wavelength cancels the transverse contraction and reduces the on-axis contraction to g. So they were wrong. |
STANDING WAVE CONTRACTION

beta = 0 g = 1 Standard standing waves. No contraction.
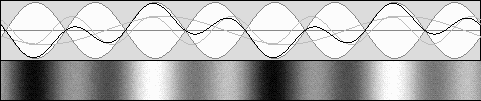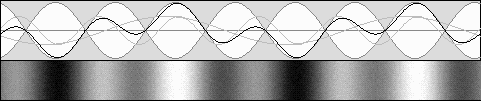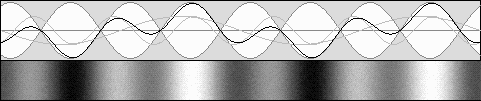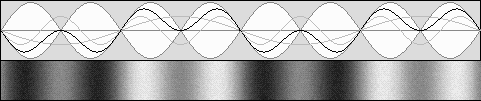
Mr. Yuri Ivanov's "Lively standing waves" showing nodes and antinodes motion and contraction.
beta = .5 g = .866 Same frequency, contraction to 75% according to g 2.
Here, the observer is at rest with respect to the wave medium.
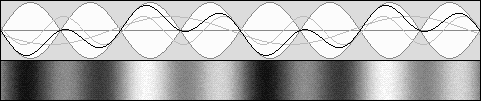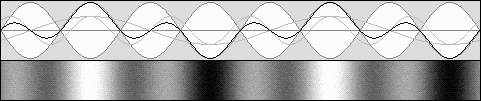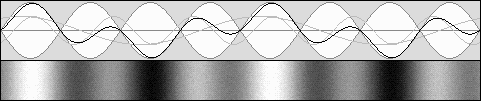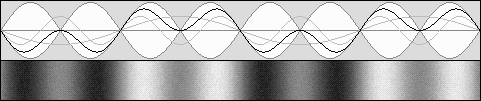
beta = .5 g = .866 Same frequency, contraction to 75% according to g 2.
Here, the observer is moving with the system's frame of reference.
beta = .707 g = .707 Same frequency, contraction to 50% according to g 2.
|
At last, a plausible explanation. In 1892, George F. FitzGerald postulated that Michelson's interferometer should contract in order to cancel the phase shift. He also tried to explain this phenomenon by aether's pressure. His discovery was never published (FitzGerald was not sure) and Hendrik A. Lorentz also independently discovered that matter should contract. Using Voigt's equations, he also discovered a time effect. FitzGerald and Lorentz were unaware of matter's wave properties, but it is a well known fact since de Broglie's discovery. From this very moment scientists could establish a relationship with standing wave contraction, but they never did. Today, one can postulate that matter is made purely out of standing waves. Then Michelson's interferometer should indeed contract and cancel the phase shift because light waves behave exactly the same way as matter waves do. In 1904, Lorentz and Poincaré finally found the correct g contraction value, which produces no transverse contraction any more. They showed that a time shift should occur, and that moving clocks should also slow down. These are the Lorentz transformations. Lorentz's equations are famous today because they led to Relativity. Matter is made of standing waves. Without any frequency change, it should contract according to Michelson's calculations: Standing wave axial contraction: according to g 2. Standing wave transverse contraction: according to g. However, because its frequency should slow down according to g, the basic wavelength is increased according to 1 / g. Transversally, one obtains: g / g = 1 and there is no transverse contraction any more. In the direction of motion, the g squared contraction is reduced to g. Finally: Matter on-axis contraction: according to g. Matter transverse contraction: none. |
|
The Michelson interferometer undergoes a length contraction in the direction of motion according to Lorentz's g factor. |
THE LIGHT BEAM LENGTH CALCULUS
|
The animated diagrams shown above indicate that for one third of the speed of light, the interferometer arm's length must be about 4 wavelengths in order to obtain the phase opposition. This length must be greater for smaller speeds. So Michelson had to build a very large interferometer. Michelson's calculus was rather complex because he considered the relative speed of light. One can more easily obtain the same arm's length using the standing wave compression method. Theoretically, the calculus must take the slower frequency into account. So, in the absence of contraction, the correct formula for obtaining two beams in phase opposition using the computer should be: According to the absolute wavelength at rest: L = lambda / 4 g (1 – g) However, Michelson was unaware of the Lorentz transformations, hence the slower frequency. But surprisingly, his measurements for the yellow light wavelength would remain unchanged at any speed. Because the frequency does change, the formula above simplifies to: L = lambda / 4 ( 1 – g ) Example. Let us suppose a g = .9 contraction. Then beta = .4359 and 1 – g = .1. The formula yields 2.5 wavelengths, or 5 half-wavelengths. The plane mirror produces standing waves and the distance between two nodes is one half of a wavelength. The goal is to make a node coincide with the nearest antinode. One may add that, from Michelson's point of view, moving the mirror only a quarter of a wavelength produces a full phase opposition because of the go and return trip. So only a quarter of a wavelength difference is needed:
If g = .9, the first phase opposition occurs for 5 half-wavelengths.
The worst of scenarios. The speed of the sun through galaxies all around us has been estimated to be about 300 km/sec. It could be its absolute speed through aether, but it could also be much faster. If beta is 300 / 300 000 = .001 the Lorentz contraction factor is .9999995 and the formula yields 500,000 wavelengths. So 500,000 times .0006 (yellow light) is 300 mm or 30 cm (about one foot). This suggests that a one foot tall interferometer should be enough in most cases. However, Michelson preferred to play safe. The sun being perfectly at rest, which is highly improbable, the speed of the Earth would still be 29 km/sec (about 18 miles per second). So he preferred a rather large interferometer according to the following values:
The formula indicates 1 / 4 (1 – g) = 53,419,000 times the wavelength. So the arms' length should be 32,000 mm or 32 meters (105 feet) in order to detect the Earth's minimum 29 km/s speed through aether. Michelson added many mirrors in order to elongate the total light trip. The arms' length for the 1887 experiment was 11 meters (36 feet). This should have been enough because one does not really need a full half-wavelength phase shift. Edward W. Morley tried again in 1902 with a longer 32 meters (105 feet) interferometer and the null result was confirmed. |
THE KENNEDY-THORNDYKE EXPERIMENT WAS A MESS
|
Believe it or not, one arm in Michelson's interferometer is useless. It can be omitted like this: |
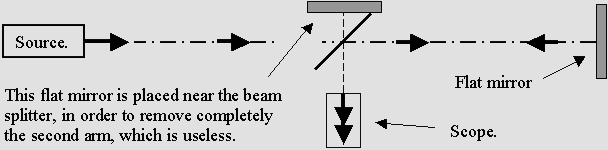
A simpler interferometer.
|
Planes can be identified, but waves must be compared because they are all identical. The comparison does not produce an immediate result and Michelson had to rotate the apparatus in order to observe the difference in the interference fringes. So the length for the shorter arm is optional because it is used only as a reference. This is not what Kennedy and Thorndyke thought. They claimed that different lengths would reveal the aether wind in spite of the contraction. So, because the Kennedy-Thorndyke experiment still ended with a null result, scientists deduced from it that aether does not exist. This is weird: believe it or not, nobody could correctly calculate the arms' lengths! It should be pointed out that the Lorentz transformations do not solely involve a contraction. The time equation also predicts that any periodic phenomenon should be slowed down in accordance with Lorentz's contraction factor. This means that the basic wavelength becomes longer. Then, whatever the shorter arm's length, the correct length formula for the longer one remains: L = lambda / 4 (1 – g) Quite simply, because it is made of standing waves, matter must contract exactly the way its standing waves do. The consequence is that any length yields a null result. Today, scientists still think that the Kennedy-Thorndyke experiment ruled out matter contraction. Once again, this is totally false. Clearly, Kennedy and Thorndyke were wrong. |
LORENTZ'S ANGULAR ABERRATION
|
Some authors noticed that the 45° angle for the beam splitter cannot be constant because of the Lorentz transformations. Any contraction would cause it to be tilted in accordance with: arc tan (1 / g). Then, because of the well known opticians' equal angle law, the beam could not be reflected along the orthogonal axis according to a 90° angle any more. The point is: this equal angle law is false inside a moving frame of reference. Lorentz himself discovered that a special "angular aberration" should occur. So he wrote to Michelson, who agreed and changed his calculus. Lorentz probably applied Huygens' Principle, which postulates that any wave can be seen as billions of "wavelets". Huygens' Principle. This web site does explain light by such wavelets, but this detail is not relevant here. However, one must admit that those wavelets should be spherical. Obviously, their center of curvature should remain at rest inside aether. Lorentz noticed that any abnormal deviation could invalidate Michelson's calculus. Some authors are misleading because they speak about Bradley's stellar aberration. This phenomenon occurs when the emitter and the receptor speed is not the same. The aberration is different here because the light source moves at the same speed. One should observe carefully how those wavelets behave in the animation below. According to Huygens' Principle, they reinforce themselves along their common envelope, and this produces a wave front. The absolute speed is worth half of the speed of light: beta = 0.5 and g = .866. The mirror angle is increased to: arc tan (1 / g) = 49.1066° because of Lorentz's contraction, but surprisingly the wave front is still deviated according to a 90° angle. The Doppler effect accounts for Lorentz's 30° theta angle. This means that waves traveling crosswise are tilted according to this angle, the same way as the planes studied above must be. |
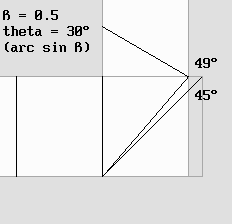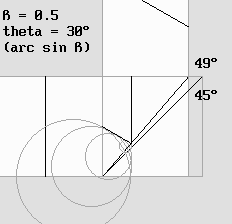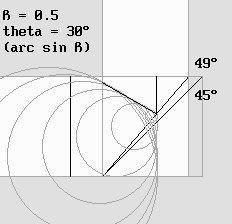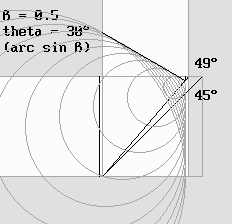
The 49° mirror angle still produces a 90° deviation.
|
Additionally, one can now experiment such phenomena in Philippe Delmotte's amazing Virtual Aether. Using my Ether19 program, I made several mpeg-4 videos showing how the light waves behave in the vicinity of the beam splitter: Michelson_axial_forward_51_angle.avi Michelson_axial_forward_45_angle.avi Michelson_axial_backward_51_angle.avi Michelson_axial_backward_45_angle.avi Michelson_orthogonal_forward_51_angle.avi Michelson_orthogonal_forward_45_angle.avi Michelson_orthogonal_backward_51_angle.avi Michelson_orthogonal_backward_45_angle.avi Michelson_orthogonal_unmoving_45_angle.avi It should be emphasized that those experiences are much better then Michelson's, because one can truly see what is going on inside the interferometer. The Virtual Aether shows that Lorentz was right: the angle can no longer be 45° at high speed. But surprisingly an angular aberration occurs which maintains the light beam reflected to a 90° angle. It is absolutely amazing! |

On the right, the unchanged 45° mirror angle produces an incorrect reflection angle.
On the left, the contraction according to Lorentz works perfectly.
Note that upward transverse waves are tilted according to the theta angle like the planes shown above.
Moreover, the transverse light beam also contracts according to Lorentz.
Clearly, Lorentz was right!
|
The Lorentz transformations are decidedly a fantastic phenomenon. They always prove to be correct. A dramatic argument. So the 45° aberration is no longer an objection. It is rather a spectacular confirmation. On the one hand, the apparatus undergoes a contraction which cancels the waves' speed difference. On the other hand, the beam splitter angle is increased in order to deviate the light beam in the correct direction. Finally, waves arrive in the scope without any phase difference. This explains the null result. Many authors, even sometimes highly respectable and well known scientists, still think that Michelson's experience ruled out aether. Such people are "Panurge's sheep". They studied physics but just memorized and repeated what their professor said. They did not verify. They forgot Descartes' maxim: doubt is the origin of wisdom. "Dubium sapientiae initium"
|
![]()
LORENTZ WAS RIGHT
|
The interferometer really undergoes a contraction in the direction of motion. Lorentz's explanation was the right one, but nobody believed him. All scientists preferred Poincare's version and Einstein's special theory of Relativity, which predict the same effects but negate the absolute point of view. This was an enormous mistake. There is a mechanical explanation for all phenomena. This includes gravity, light, magnetic and electrostatic fields, nuclear forces, etc. The absolute point of view is important because the goal is to explain what is really going on. Otherwise scientists will stay ignorant forever. |
|
One must firstly postulate that aether exists and that matter really transforms according to its absolute speed the way Lorentz showed. Then the goal is to establish carefully how a moving observer sees phenomena from his own frame of reference. The result is Lorentz's Relativity. |
|
Relativity is not complicated. It is not a mysterious theory any more. It is a law of nature. The next pages show that it can be deduced from elementary calculus, especially the Lorentz transformations and the Doppler effect. The main difference from Einstein's concept is that any moving observer is wrong about his situation, while one at rest sees phenomena the way they really occur. The moving observer also thinks that he is at rest because he sees the observer at rest undergoing the Lorentz transformations. Finally, nobody can tell for sure who is really moving. So the main difference is that the one at rest only is right. Einstein postulates that they are both right. His Special Relativity cannot explain the difference between appearances and reality. So it is false. Lorentz's Relativity can predict the same phenomena and it can also explain them. This is an important improvement. Starting from now, scientists will be able to mechanically explain matter and all physical phenomena. The aether thus should be rehabilitated. It was banished wrongfully, and it proves to be essential. Matter transforms the way Lorentz explained. This web site explains matter and all physical phenomena from a mechanical point of view. This is no longer a theory which will be confirmed some day. It is a verifiable fact. At all events, there is at the present time only one logical explanation:
Conclusion. Matter mechanics must be explained. Because matter contracts the way Lorentz predicted, and because standing waves also contract in a similar way, scientists must examine the possibility that it could be made of standing waves. This is obvious. |
| 01 | 02 | 03 | 04 | 05 | 06 | You are here. | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
|
Gabriel LaFreniere, Bois-des-Filion in Québec. absolu2000@hotmail.com On the Internet since September 2002. Last update December 9, 2007. |