
Standard plane standing waves.
Note that the amplitude between each peak is always null. Such places are called nodes. The peaks are called antinodes; they are present "two" times per period and "two" times per wavelength. However, the medium pressure alternates between a minimum and a maximum inside both of them. Standing waves certainly are one of the most neglected domains in physics. One can identify many misunderstood characteristics. For example:
Scientists seldom mention them. They prefer to spread out their knowledge with a lot of complicated equations. This is sometimes quite useless. For instance, many diagrams from this site were simply displayed by computer using sine functions only. Others were made using Huygen's Principle, without the help of equations. The
energy equals the square of the amplitude. Two sets of waves will add
their amplitude, and this means that while the phases are adding
constructively, the energy is four times higher there.
This explains why billions of waves which mix together will not cancel
their energy in accordance with the Great Numbers Law.
Standing
waves do not contain waves traveling in opposite
directions. Two
sets of plane parallel waves traveling in opposite directions will
indeed produce plane standing waves. One may place a plane parallel screen in the
way of just one set of plane traveling waves and also obtain standing
waves. Other methods are possible. In
addition, the above animation shows two waves traveling in opposite
directions. From a mathematical point of view, one then can add their amplitude
and obtain the classical standing wave pattern. However,
it should be emphasized that although this method works, it is only an artificial
one. This is not what is really going on. The Huygens Principle
also works, but it does not mean that regular waves contain spherical
wavelets. One should realize that when standing waves are present, the
medium does not behave in the same manner as for traveling waves. Inside
standing waves the energy is alternately transferred from kinetic energy
to pressure energy, in accordance with Hooke's law. The medium behaves
like a spring section moving to and fro. Inside regular traveling waves
both types are present simultaneously and constantly move at the same
speed. On the contrary, there is no energy transfer inside standing
waves. Finally, when lossless standing waves are present inside a
finite space, such waves will theoretically continue to oscillate
eternally. Because all standing waves actually will lose some of their
energy, they need replenishment. So any amplification process can prevent them from fading out. I
had much trouble explaining this to many people. They could not
understand that the electron, which is a spherical standing wave system,
does not need "in-waves" in order to be replenished. The
electron was certainly created billions of years ago from such in-waves. But today it
already exists. The amplification process now allows the system to go on
oscillating permanently.
PSEUDO STANDING WAVES or MOVING STANDING WAVES or LIVELY STANDING WAVES Waves emitted by a moving device will undergo the Doppler effect. Let's suppose that its speed is worth half of the speed of light. Then the beta b speed value is worth v / c = .5. The Doppler effect equals 1 – b = .5 forward and 1 + b = 1.5 backward. The wavelength ratio will be 1.5 / .5, hence 1 : 3.Surprisingly, using such waves, and as compared to the diagram shown above, the wave patterns will be contracted to 75% of their normal length. Moreover, nodes and antinodes will move forward and their speed will be equal to the same .5 c beta speed. |
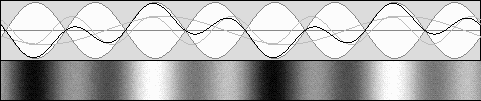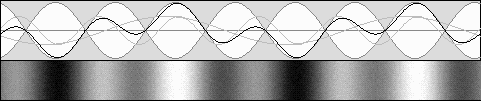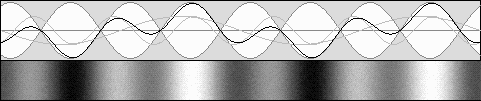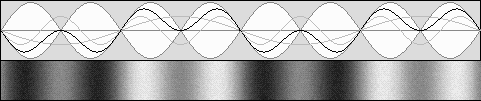
Standing waves motion and contraction.
This phenomenon may have been discovered by Mr. Yuri Ivanov in 1990. http://www.keelynet.com/spider/b-104e.htm http://www.keelynet.com/spider/b-111e.htm Mr. Ivanov did not understand the Lorentz time transformation and proposed his own transformation with t' = t similar to Michelson's calculations. According to Lorentz the wavelength is increased because the overall frequency is slowed down. Finally there is no crosswise standing waves contraction: Mr. Ivanov's system is wrong. I don't agree with his spider or levitation effects, either. Anyway, let us examine standing wave's contraction first. In order to observe the above diagram in a more easy and intuitive manner, here is the same diagram as shown above, except for the observer who now follows the apparently unmoving nodes and antinodes: |
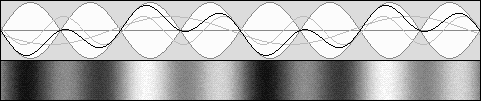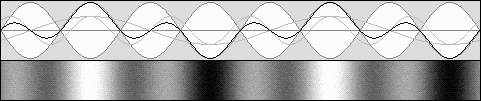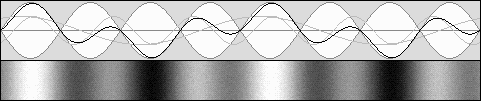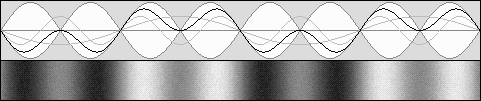
Here, the observer moves towards the right. Now, nodes and antinodes seem to be immobile.
Three times longer waves seem to move three times faster, explaining the same wave rate or apparent frequency.
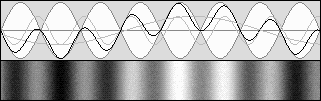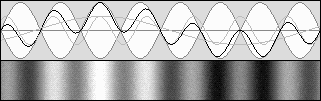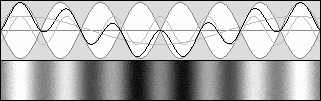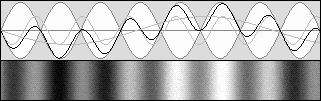
STANDING WAVES CONTRACTION
g = (1 – b 2 ) (1 / 2)The beta b speed value equals v / c. So the wave patterns should be contracted like this: |

b = 0 and g = 1. No contraction.
System at rest: 0 c. No Doppler effect.

b = .5 and g = .866 Contraction to .75 according to g 2.
Doppler leftward: 1 + b = 1.5 Doppler rightward = 1 – b = .5
b = .7071 and g = .7071 Contraction to .5 according to g 2.
Doppler leftward: 1 + b = 1.7071 Doppler rightward = 1 – b = .2929
Standing waves also undergo a less severe contraction according to the g value (not squared) on any transverse direction (see below). However, Lorentz also showed that the system frequency should be slowed down according to the same g value. This means that the electron should finally undergo the contraction on the displacement x axis according to the g value not squared. And there is no contraction at all on both y and z axis. This is the Lorentz distance contraction. This explains why matter, which is made of standing waves, should also undergo the Lorentz transformations. This also explains why Michelson's interferometer did undergo such a contraction and could not reveal the aether wind. |
PARTIALLY STANDING WAVES
(Unequal amplitude)
|
The animation below shows standing waves where compressed waves are two times stronger. Such standing waves evolve inside a very peculiar envelope which looks like a peapod. |

Partially standing waves: E1 = 67 %, E2 = 33 %, b = 0
PARTIALLY MOVING STANDING WAVES
(Unequal amplitude and wavelength)
|
This is the general case of electrons. These pages show that stronger aether waves can "push" an electron. This is the radiation pressure, which can be explained by "partially moving standing waves". In the animations below the waves' amplitude differ but there is also a Doppler effect. Such waves still evolve inside the same peculiar envelope, whose speed remains exactly the same as for equal amplitude waves. Note that nodes are partially hustled sideways; any stronger wave will act in the same manner on any sort of standing wave systems. So it will push the electron's central antinode. |
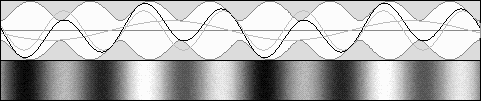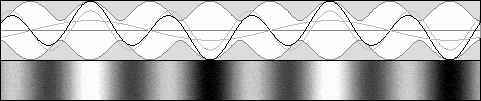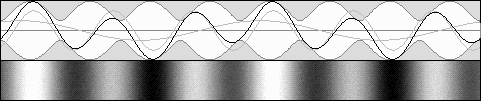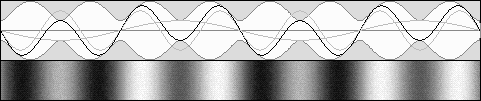
Partially moving standing waves. Forward contracted waves are stronger.
E1 = 67 %, E2 = 33 %, b = .5
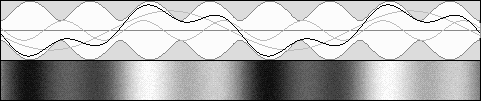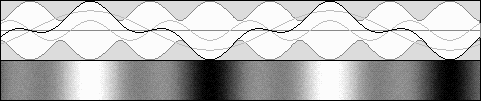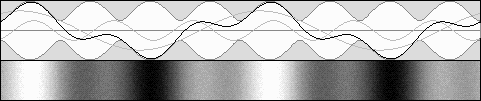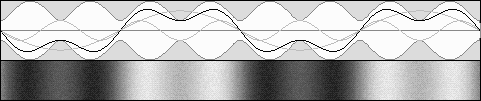
Partially moving standing waves. Backward dilated waves are stronger.
E1 = 33 %, E2 = 67 %, b = .5
TILTED WAVES TRAVELING ALONG A TRANSVERSE AXIS
|
Let's imagine two train cars at rest along parallel railways. Their flat sides can reflect sound waves so that one can produce standing waves between them. However those waves must travel according to an angle in order to follow the cars while they are moving. This is Lorentz's theta q angle, which equals: arc sin b. So two sets of waves traveling in opposite directions will undergo a scissor effect.Moreover, Michelson showed that such trains would not accept the same resonant frequency at high speed any more because the wind will decrease the apparent speed of sound . Such waves behave in a very strange way. So I first showed in the left animation below those trains traveling rather slowly : 10 % of the speed of sound (76 mph). The scissor effect is obvious. The Time Scanner Page explains that the intersection points follow the places where Lorentz's t' time does not change. Scanning this diagram right on those points would produce standard plane standing waves.
|
|
|
|
Left : 10 % of the speed of sound. Right : 50 %.
The animation on the right shows the trains traveling at 50 % of the speed of sound (380 mph). Then beta = .5 and the waves will be tilted to : arc sin beta or 30°. Surprisingly, this system seems to move sideways. A "checkerboard effect" moving sideways is even more visible in the more sophisticated animation below, which however shows the same situation:
|

Transverse standing waves : v = .5 c.
Transverse contraction to .866 according to the Lorentz g value.
However, no contraction actually occurs because the frequency also slows down according to g.
It should be pointed out that such transverse standing waves still do not contain two sets of traveling waves moving in opposite directions. This is a completely new and different wave system where the medium pressure alternates from one point to another. Now one may speak about energy transfer, whose speed is that of the system. This was also the case for longitudinal "moving" or "lively" standing waves. The time shift will cancel the checkerboard effect. Now let's suppose that you are a bat. Instead of seeing objects by the mean of light, you can "hear" objects so well that you will actually see them. What will you see if you are moving on the top of these trains ? The answer is : you will "hear" regular standing waves. They will not appear tilted any more. You will not see a checkerboard moving sideways because the sound is traveling three times slower while it is coming from the rear through the wind. So the information travels much faster if it comes from the front of the train. This also produces a "time shift" when you are observing with your ears a clock placed at the front of the train and compare it to another one at the rear. Henri Poincaré discovered that clocks will not indicate the same hour along a moving system in order to preserve the apparent simultaneity. This happens with light too because we see things with our eyes, by means of light. Such information IS NOT simultaneous while we are moving through the aether, and so we encounter the same effect as you did, as a bat. According to Poincaré the time shift equal: b / (1 – b 2 ) in absolute seconds for one light second distance. A beta value of .5 produces a time shift of .666 second per light second. A light second is worth 186,000 miles (300 000 km) and it is about the distance to the Moon. This means that moving at .5 c a clock on the Moon should be about .666 second late if it was in the front of the moving frame of reference. The pages on Relativity propose a more dramatic example : a speed as fast as 86.6 % of that of the light. Then objects and distances are contracted to 50% of their original at rest length. The animation below shows that inside such a frame of reference moving to the right, a plane wave emitted very far away on the CD axis will be tilted to as much as 60°. However, any observer placed on this axis will think that observers A and B did receive this wave at the same time. This will "prove" that this wave is not tilted : |
|
|
A tilted wave seems parallel to the displacement x axis in a moving frame of reference.
Bradley's star aberration is not noticeable while both the Earth and a distant star are moving together.
Any observer on Earth will only record the speed difference.
Next page is on Spherical Standing Waves.
| 01 | 02 | You are here. | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
|
Gabriel LaFreniere, Bois-des-Filion in Québec. Email: Please read this notice. On the Internet since September 2002. Last update September 26, 2007. |