離散的なドーナツはチェーン"ddtc"をねじりました。 スペースと事柄のモデル リチャードL.マーカーで

フレームを使用するために: http://www.ncia.com/~rlmarker/ddtc.htm    
どんなフレームにもそうしません: http://www.ncia.com/~rlmarker/ddtcall.htm

Abrikosovフラックス格子 超伝導体の渦コア州 礼儀AT&T、ベル-研究室 Copyright AT&T、1995 ベル-研究室

次の絵

超伝導体UPt3の渦格子

礼儀ダリル・ヘス博士

凝縮した物質と放射、NRL

NRLイメージギャラリー

次へ

彼の普通の位置のリッシュ

 
「あなたがそうするならば、本当の真理の探求者になってください」
あなたはあなたの人生の少なくとも一度そうしなければなりません。
「万物をできるだけ疑ってください。」
 
Renデカルト
Discours de la M騁hode、1637。

次へ

記述:	離散的なドーナツ撚り合わせているチェーンモデルはスペースに関するボトムアップ説明を提供します。 Ddtcは何に答えるか、そして、なぜとその方法は力と粒子に関して質問されるか。
キーワード:	「リチャードMarker、ddtc(重力)はチェーンをねじりました、電子、スペース、料金、トーラス、ドーナツ、事柄、時間、量子、マーカー、粒子、物理学、微細構造、クォーク、磁気です、フリーエネルギー、「スーパー-結」しています、表皮効果」

加速MSインターネット・エクスプローラーをほのめかしてください:
Viewオプション一般設定にページを決して再ロードしないように設定してください。
次に、あなたが呼び出したがっているときはいつも、再ロードが使用を呼び出す、ボタンをリフレッシュしてください。

次へ

主なインデックス:

a。   他のリンク	5.   神秘主義的な定規を調節してください。
b。   版権情報	6.   10の寸法
c。   序文	7.   左か右の宇宙?
d。   ddtcは何ですか?	8.   Ddtcの詳細と計算
0.   概観	9.   ddtcからの思惑
1.   ddtcは肉体的に本当ですか?	10.   フィードバック
2.   時間は何ですか?
3.   重力質量はどのくらいですか?
4.   どんな原因が請求されますか?

新しいです: 直接138チェーン長さの計算に行ってください。

戻ります。

電流

次へ

a。 他のリンク:

ずば抜けたイメージ:	ベル-研究室のギャラリー
代替の理論のために:	究極の物理学--- リンク
大きいエーテル理論サイト:	ブラウン教授のウェブサイト
他の代替の物理学:	Yahooウェブサイト
重力の速度:	トムバンFlandern、メリーランド州の大学

通知してください。  ウェブマスター リンクがアップデートを必要とするならば

戻ります。

電流

次へ

b。 版権情報:

Copyright1996-2001

リチャードL.マーカー

ヴァーノン山、WA 98273

All rights reserved

この記事は、非商用目的のためにその全体だけで他のものにコピーされて、配布されるかもしれません。 この印刷された公表をこのドキュメントか部分が単独かいかなる他のドキュメントの一部として記録して、禁止されている一かたまりにしてください。作者の急行許可書。 この版権情報はコピーか部分的なコピーが分配したいずれでも完全に保たれなければなりません。

戻ります。

電流

次へ

c。 序文:

作者は、20年の期間にわたって1978年に始まりながら、Discrete Donut Twisted Chain Theory(ddtc)を開発しました。 理論の基本形は初年度の間発生したが、1996年に初めて、役に立つ計算は可能になりました。 多くの平行線が存在したが、理論は別々に主流の理論から発達しました。 これは新しくて肥よくな地面です… ざんごうを掘ってください!

戻ります。

電流

次へ

d。 "ddtc"スペース/事柄モデルは何ですか?

スペースと事柄のほとんどのモデルが観測された現象に関する説明として「トップダウン」から発達します。 "Ddtc"はスペース、事柄、および時間の本質に関する論理的な説明として「ボトムアップ」から発達します。 ddtcモデルは観測された現象に従います。 既存のモデルはスペース、事柄、および時間の本質に関する論理的な説明を提供しません。 彼らは、粒子と力運送業者を定義するために多くの成分を当てにします。 既存のモデルは成分に共通の、そして、理解できる構造物に変えません。 本当に、力は単に力キャリヤー粒子の交換から生じます。 既存のモデルは力を運転することか粒子を作成することに関するどんな詳説も提供しません。 すべてのモデルが現実の本質に関する仮定から発します。 ddtcモデルは非常に簡単な仮定から発します: スペースのあらゆる要素が「何か」か「何でもない」から成ります; 「何か」が存在しているならば、存在し続けます; そして 2「somethings」がたまたまお互いに遭遇すると、単に反対している動きを平均することによって、彼らは互いに影響します。 次へ 俗人はddtcを理解することができますか? 多くの俗人が、ddtcの基本的な操作が理解できるのがわかります。 大部分は、モデルを開発するか、または推定するのにかかわる物理学か数学のどれかを避けるのを選ぶでしょう。 物理学者はddtcを理解することができますか? 彼らが自分たちにかかわった過程を探らせるならば、物理学者はddtcを理解することができます。 物理学者は、探検のためのはるかに良いツールを持っているが、多くの先入観をまた持っています。 オープンでせんさく好きな心は最もよく働いています。 Ddtcは学ばれなければならないいくつかの新しい概念を含んでいます。 それをあなたの非ddtc視点に広げるのを試みる前にあなたはddtc視点を学ばなければなりません。 視点は敷衍されるが、あなたは、早くに跳ね過ぎることによって、ポイントを逃します。 標準の物理学はddtcを理解するのに必要である概念のすべてを所有していません。 Ddtcは少しもinputted定数なしでモデルの幾何学に純粋に基づく具体的な答えを提供します。 それは遠くにvauge概念を越えます。 驚くべき美と構造はddtcの簡単な始まりから発達します!

戻ります。

電流

次へ

0.  概観

Ddtcは接続ドーナツチェーンとしてスペースと事柄の織物を記述します。 チェーンの各リンクは「ドーナツ粒子」(唯一の粒子)によってドーナツの表面の周りの螺旋状の経路を旅行しながら取られる経路から発達します。 パイ/2ねじれ(4分の1回転)があるチェーンセグメントは料金を作成します。 ddtcモデルはドーナツ粒子経路である輪での最高のストリングループ・モデルに類似しています。 時間を含んでいて、ドーナツには自分たちの上で輪にされるドーナツの10の寸法、3つの標準の空間的な寸法、1つの時間の寸法、および6つの寸法があります。 ドーナツ粒子経路の分離性と幾何学はinputted定数かどんなユニットにもかかわらない基本概念から重力の計算を電磁力の比まで許容します。 最高のひも理論を解決するキーはドーナツ粒子衝突のフェーズとそれらの衝突角度の最小化にかかわります。 衝突のフェーズの要件は素数を重要な考慮すべき事柄にします。 次へ 計算の重力に、どんな瞬間にもドーナツ経路に沿ってドーナツ粒子の正確な位置を知っているのは決定的です。 連続しているか、またはドーナツの正確な離散的なフォームを欠く理論が重力を解読するのにおいて不可能に思えます。 連続した構成の離散的な実体として全体のドーナツチェーン・リンクを扱うのは不足します。 それぞれの個々のリンク(ドーナツ)は離散的な粒子が旅行する経路として見なされなければなりません; 連続のリンクとして見なされるよりむしろ。 このドーナツモデルをより大きいスケールを作動させる他の螺旋状のモデルに間違えないでください。 例えば、電子は封鎖グループのドーナツチェーンの周りを移動します。 この全体の接続チェーンは、螺旋状の方法でねじれていて、ある他のモデルのドーナツに類似しています。

戻ります。

電流

次へ

1.  ddtcモデルは肉体的に本当ですか?

このモデルにおける物理的性質は単に起こる過程への類推ではなく、本当の過程であると作者によって信じられます。  ddtcモデルはその開発においてほとんどのモデルと異なっています。 数学的モデルか機能を観測された物理的なデータに合わせるよりむしろ、このモデルは論理的な形而上学のアプローチ(宗教感覚ではなく、思考実験意味における)から発達します。 モデルの地盤は、したがって、それらのように「それが何であるかということです」をしてくださいというように「それがそうである理由」に同じくらいたくさん答えます。 本当に、この「下部の上」方法からアプローチされない場合、スペースの離散的な本質の重要な一面は手が届かなく見えます。 読者は、このモデルが、一般的で特別な関連性の周りと、そして、動きの安定した経路の周りで一般通念から出発するように見えるのがわかるでしょう。 作者は一見したところでは結論か論理のいくつかの外観上の不条理を認めます。 外観が示される限り、これらの出発はさ迷いません。 しばしば、ddtcは単に標準の現象の代替の視点を提供します。 あなたのそれより複雑なこの材料の協定をしないでください。 どのようににかかわらず概念、外国、簡単であって、わずかであるか。 あなたが正しい過去に問題の心を容易に駆け出させることができるくらい簡単です。

戻ります。

電流

次へ

2.  時間は何ですか?

時間はddtcによって基本的です。 主軸に関するドーナツ粒子のそれぞれの主要な革命は現地時間のユニットです。 隣接しているドーナツは非常に密接に互いに連動します。隣接しているスペース時計につなげられるスペースでそれぞれのドーナツ粒子で作られる スペース時計であると考えることができる「ギア機構」を内部連絡する巨人を形成します。 隣接しているクロックスピードの違いは時間の肥大と重力を形成します。 ドーナツチェーン織物の存在の前に、用語「時間」はあいまいな意味を持っているように思えるでしょう。

戻ります。

電流

次へ

3.  重力質量はどのくらいですか?

すべての 固まりが料金の料金か動きから生じます。 少なくとも電子に関しては、主な角張っている回転の異なった比率に、速度(ドーナツセンターの周りの)を二次回転速度に採用するドーナツ(ドーナツ縁の周りの)によってドーナツチェーンにおけるねじれは隣接しているドーナツでゼロに接触角を再編成する試みで補われます。 採用される安定したパターンは全くゼロへの接触角を閉じるというわけではありません。 結果として起こるわずかな接触角は単に互いを平均してくださいて、非常にわずかなこの 接触抗力のためドーナツ粒子速度を 遅くしてくださいというわずかな反対している動きをもたらします。 特定の本当の粒子を構成する接続のためのすべての接触歯止めの合計はその粒子の集合 粒子時間の抗力(すなわち、粒子のために様々な接触歯止めを同封する表面へ不可欠な状態でまとめられた時間の肥大)を作り出します。 簡単な角張っているドーナツチェーンねじれと同様に粒子動き(回転であって翻訳の)が接触抗力に加えるのに注意してください。  ドーナツタイム・ユニットはドーナツの周りで1回の革命をするのにドーナツ粒子を要する時として扱われます。 遠方の粒子の契約抗力によって引き起こされる 時間の肥大における ドーナツ距離(すなわち、ドーナツユニット距離)の上変化はその粒子から生じる 時空の加速「そり」を生産します。 次へ 接触抗力の計算は、経過した数を合わせるのをドーナツ革命を隣接しているドーナツの間の接触まで要求します。第一の回転数と二次回転速度と共に。  接触が達成される前にこれらのすべての3つの数が一致してい なければなりません。 フェーズでは、接触が超弦理論の前に知られていなければならないキーであるように思えるので、ドーナツ革命の経過した数は重力について計算するために働くでしょう。 旅行されるドーナツ経路は 連続 したストリングではなく、単にドーナツ粒子の経路です。 後のセクションにチェーンセグメントが主な電子ドーナツのこの数の計算を含んでいて、素数が重要な役割を果たすのに注意してください。 大規模計算が示す電子の重力が光の速度の4.65E+34およそ倍を旅行する現状! しかしながら、それは波として旅行しません。 重力は、接触で単に隣接しているドーナツ粒子の「時計」時間を平均するのから非常に効率が悪く、結果として生じます。 我々がそれを知っているようにエネルギーが累積している抗力によって決定するのではなく、時間がたつにつれてスペースの時計の上でドーナツ構成で決定するので、この非能率は物理学における、我々のエネルギーの標準の測定に影響しません。

戻ります。

電流

次へ

4.  どんな原因が請求されますか?

ドーナツチェーンセグメントをねじるので、結果を 告発してください(料金分野ではなく、料金ソース)。 よりを戻しているチェーンセグメントから取り外されるドーナツは、隣接しているドーナツチェーンセグメントに再接続するためにねじれを必要とします。 スペース織物は 長い間強い力の範囲の外の138個のドーナツである ドーナツチェーンセグメント から成ります。 あなたが最短距離はあなたがするあらゆる添加か取り外しのために再接続する必要があったドーナツチェーンセグメントをねじると仮定すると、 ドーナツリンクの取り外しが負帯電型か添加a正帯電型を作成するでしょう。 したがって、非請求されたドーナツチェーンの長さが138であり、あなたが1個のドーナツを取り外すと、結果として起こる長さの137は負帯電型を運ぶでしょう。 非請求された長さが136であり、あなたが1個のドーナツを加えると、結果として起こる長さの137は正帯電型を運ぶでしょう。 電子はスペースを通って1個のドーナツで移行するスペースとの先端の関係によって動きます。 これは、次のチェーン(新しい電子)を短くして、現在のチェーン(古いelctron)を伸します。 接続の流れはひずみを軽減するためにスペースを通って移動するドーナツのストリングによって代償されるスペース織物におけるひずみを引き起こします。 この流れは磁気ベクトル・ポテンシャルと同系です。 高周波が導体の皮膚だけの中を伝わるところで「表皮効果」はドーナツが電子が導体を通して流れるようにスペースを通って移動する直接必要性に関連します。 高周波では、導体の電子流とスペースでの補足的なドーナツ流動はわずかな深さを導体に理解する時間を持っているだけです。 必要なドーナツ流動が導体により深く浸み込むことができる時までに電子流圧力は既に指示を逆にしました。 139と137が構成する事実はフェーズにおける介入しているモードが、よりありそうでないので第1が電子の安定性に加えるということです。 (、用意された組に関して、見てください、「、鏡には、ふたり顔があります--、バーバラ・ストライサンド、」、私の好きな映画人をcoincidentlyします。 ストライサンドさんはどのように用意された組の重要性がわかりましたか?! 言う、彼らの尻を出して、彼女がいくつかの創作のためにあまりに豊かに値するオスカーを彼女に与える気さくな南部人)

戻ります。

電流

次へ

5.  時間、神秘主義的な定規

Ddtcはスペースで時間をギヤ(ドーナツ)の時計位置まで短縮するが、時間をすべての相互作用を制御しているマスターに登用します。 スペースのギヤが非常に密接にお互いに連動するので、それらを通る巨大な力のトランスミッションはほとんどささやき声を作成しません。 ドーナツが他のドーナツと調子外れな状態でおよそ十分ふざけるとき、我々はそれを事柄の位置に登用します。 自己中心はddtcがある冗談です。 ドーナツ粒子が、ドーナツ経路を旅行するのを学ぶ前に、時間は存在しませんでした。 ビッグバンの1秒後の第1部はddtcで意味を制限しました。ビッグバンが徐々に現在の時間の系列の始まりを作成したので。 ドーナツは宇宙を運転するエンジンです。 事柄は、それらを減速させて、スペースで徐々により遠方のドーナツを減速させます。 これらの遠方のドーナツはそれらが重力を生産するタイムワープを引き起こすために重要であるように閉じるより高いレートで回転します。 ドーナツはそれ自身の時計です。 あなたはあなたが欲しいすべての下側にそれを遅くすることができます、そして、それは時間の基準以来の元の速度がそれと一致して遅くする行くことであるかのようにまだ反応しています。

戻ります。

電流

次へ

6.  スペースには、10の寸法があります。

三次元スペースのカジュアルな用法は作者側の無邪気の外観を引き起こします。 三次元にはどんな魔法がありますか? 作者は、我々の三次元世界が、三次元スペースが唯一の答えであるかもしれないことを書き取らないと信じます。 むしろ、我々の世界が表す寸法はスペースの第一の広さで単に反射的です。 各ドーナツは3オリエンテーションとマグニチュードを持つことができる主軸を所有しています。 さらに、ドーナツ粒子が経路のらせん状の局面を作成するように、各ドーナツは回転する軸を所有しています。 これらの回転する軸も3オリエンテーションとマグニチュードを持つことができます。 これが10の寸法になる時を含んでいること。 ドーナツのいくつかの寸法が他の寸法に関連します。 第一のドーナツオリエンテーションはお互いとのチェーン関係によって制限されます。 回転する軸の二次ドーナツオリエンテーションはほとんどいつもその主軸の周りのドーナツ粒子の動きに平行でしょう。 ほとんどの計算に関しては、これがありそうな発生であるように思えます。

戻ります。

電流

次へ

7.  スペースには、利き手がいます。

反対の利き手のドーナツを接続するようにしてください。 あなたは、すぐ、隣接しているドーナツが、衝突(それらの主軸に対する通常45度における)のポイントにそれらのドーナツ粒子動きが平行であることを持つのに同じ利き手が必要であると発見するでしょう。 スペースのこの利き手は人の自然な対称の意味に違反します。 中性子のベータ腐敗はいつも同じ回転がサポートを離散的なドーナツ撚り合わせているチェーン理論のこの局面に与えている中性微子を作り出します。

戻ります。

電流

次へ

8.0  Ddtcの詳細と計算

8.1   ddtcの発展

8.2   138個のリンクのチェーンの長さ

8.3   重力対e-力の比率

8.4   微細構造定数

8.5   電子の大規模比への陽子

8.6   クォークは何ですか?

8.7   重力の時間の肥大

8.8   ddtcは関連性で働いていますか?

8.9   ドーナツはどれくらい大きいですか?

戻ります。

電流

次へ

8.1  ddtc構造の発展:

仮定が主にこのモデルの結果に導く1つ。  距離の小にかかわらず空きスペースを通ってどんな力も伝えることができません。 衝突すると、相互作用はドーナツ粒子の反対している接触動きだけの間に起こります。 Ddtcは、宇宙が 空きスペース(すなわち、 すべての不在、空間)に住んでいる ドーナツ粒子と呼ばれる単独の粒子タイプから成ると仮定します。 ドーナツ粒子は特別な特性のない「何か」のただ一つの要素です。 それが簡単さのための丸い一定のボールであると仮定してください。 また、作者が「空きスペース」と対照的に真空について言及するために単独の用語「スペース」を使用するのに注意してください。 らせんの経路に沿った離散的な ドーナツ粒子旅行は、 ドーナツの総合的な形を形成するためにそれ自体で巻きつけられました。 隣接しているドーナツは ドーナツチェーンのリンクを形成します。 関連スペースのすべてのドーナツが 正しいか、または不器用であるに違いないが、両方は不器用でないに違いありません。 これは、接触でスムーズにかみ合うように隣接しているドーナツの必要性から起こります。 正常なスペースは接続ドーナツチェーンから形成されます。 チェーン(ドーナツ)の各リンクはその主軸を隣接しているドーナツから90度回します。標準がまさしくチェーンによりを戻させたように(すなわち、同じオリエンテーションでドーナツを返すのに4個のドーナツのチェーンを要します)。 次へ ドーナツモデルは多くの結果を基本的なトーラス形(ドーナツ形)に基礎づけます。 いくつかの心理戦が、我々が、ドーナツ粒子がどのように、なぜトーラスの動態的経路形を達成するかを理解するのを助けます。 覚えていてください、そして、ドーナツのような経路はチェーンセグメントを形成するために接続するチェーン・リンクに類似しています。 これらのチェーンセグメントは、好みの座標系を構成する スペース織物を形成するために接続します。 スペース織物、チェーンセグメント、またはドーナツ経路さえ存在する前に始まる精神的な旅行を始めてください。 ドーナツ粒子は存在しました。それらが空きスペースに住んでいる「何か」であるので。 この前の段階のドーナツ粒子はその最後のドーナツ経路よりむしろ行き当たりばったりの周期的な経路を旅行しました。  それはなぜこの行き当たりばったりの経路を旅行しましたか? 空きスペースはどんな好みの座標系も全く所有していません。  加速される すべてのコーディネートしている基準方式が空きスペースの総空間で等しい状態を獲得します。 馬鹿ドーナツ粒子はそれらの位置を知りません。 それぞれのドーナツ粒子はそれ自体に比例して静止していたままで残っていました。 別のドーナツ粒子に比例して、動きは動きの どんな周期的な経路も帯びることができました。 互い(あなた方数学者にとってフーリエ級数と同様の)に上に重ねられる一連の円運動によって行き当たりばったりの周期運動を表すことができるでしょう。 動きのドーナツ経路を達成する前にドーナツ粒子動きのこの記述が起こるのに注意してください。 次へ 根本的な空きスペースの好みの座標系の非実在はドーナツ粒子動きが存在する理由です。 スペース織物が形成される前に、ドーナツ粒子はどう静止しているかを知りませんでした。 この音は総ナンセンスが好きですか? それらがddtcに通じる要所移動を含んで、あなたはreareadにこれらの2つのパラグラフが欲しいことができます。 スペースのこの扱いにくい視点は事柄を混乱させるだけであるように思えます。 本当に、1つのドーナツ粒子が別のドーナツ粒子に連絡するまで、非常におもしろいものは何も起こりません。  偶然の接触では、2つのドーナツ粒子がお互いに比例してそれらの反対している動きを平均します。 結局、より多くのドーナツ粒子が、衝突して、スペース織物の好みの座標系を作成するために反対している動きを平均します。  反対しているドーナツ粒子の平均はリードを宇宙におけるすべての変化に身ぶりで合図します。 議論している動きがドーナツ粒子だけに影響するのに注意してください。 ドーナツ粒子は直接標準の物理学粒子に対応していません。  標準の粒子と力はスペース織物を構成するドーナツ粒子のダイナミックな構成と相互作用から発達します。 次へ 我々が円運動の合計として早いドーナツ粒子行き当たりばったりの周期運動について説明したと思い出してください。 一般に、これらの2つの円だけが互いとスペース織物に比例して安定性を楽しむと判明します。 主要な安定した円はドーナツ穴の中心を通して主軸に関してドーナツ粒子動きから生じます。 主要な円の周りを旅行するのに従って、螺旋状の経路からの2番目の安定した円の結果はドーナツ粒子で続きました。 通常、安定した「非-取り消し」幾何学は、ドーナツが45度で接触線でそれぞれのドーナツの主軸に置かれるのを必要とします(すなわち、隣接しているドーナツは90度の角度に主要な軸を持っています)。 接触における非常に即時では、衝突しているドーナツ粒子の動きはお互いにほとんど沿います。 2つの第一のもの以外の円運動は結局、衝突の過程の間、取り消されます。 これは我々のモデルの基礎を形成するドーナツ経路だけを去ります。 次へ 動きの円形の安定した経路は我々の常識を偽ります。 平凡な生活では、我々は空きスペースの物理学よりむしろスペース織物の物理学を見ます。 接触がなければ、外でそれ自体でいかなるも粒子には、それが輪になって旅行しているかどうかを「知る」どんな方法もありません。 その結果、ドーナツのための 最初の議論を発生します:  動きの円形の経路は空きスペースで安定しています。 ドーナツのための 2番目の議論は必要性から来ます。  接触相互作用を押すだけがドーナツ粒子の間に起こるという我々の主要な仮定を思い出してください。 我々はドーナツ粒子が絶えずそれを押しのけないで別のドーナツ粒子に影響する方法を必要とします。 円(ドーナツ)は力を押すのが存在していて、安定している場合がある経路を提供します。 デカルトは彼が何世紀も前にした仕事で連動している円を使用しました。 作者は、彼の円がどれくらい同様であったかもしれないかを知るために、この仕事(まだフランス語の)に近づく手段を持っていませんでした。 ドーナツのための 3番目の議論は ビッグバンの視点がある一貫性に関連します。 元々、すべてのドーナツ粒子が手当たりしだいに移動していました。 ビッグバンの前に、これはありました。 粒子は、異なったサイズ、異なった利き手、および異なった「ゲージ」のスペースの小さい切り離された領域を形成するために衝突しました。 ddtcモデルで説明される正常なスペースの138ドーナツチェーンセグメントの長さは多くの変遷の後にだけ結果として生じました。 初めに、それぞれのドーナツチェーンセグメントは、様々な長さで形成したか、または結合しました。 より多くの活動(時間の通路)の後に、早くから、いくつかの安定したスペースゲージがまだ異なっていたかもしれません。  たぶんビッグバンに類似している最も近い視点は初期の構成の後にいつか起こりました。異なった切り離されたスペース地域(「ミニ宇宙」)が、より大きい領域(同じ利き手)を形成するか、または互い(異なった利き手)の一部を破壊するために互いと衝突したとき。 ミニ宇宙は結合して、数の、しかし、どんな単一の宇宙にもありそうでない合計を減少させました。 本当に、単一の宇宙は不可能であるかもしれません。 ゼロへの宇宙合計の利き手であるならば、単一の残っている右利きの宇宙と単一の残っている左利きの宇宙との最終的な衝突は両方の宇宙を破壊することができました。 これは、ビッグバンを始めながら、状態を近さに返して戻すかもしれません。

戻ります。

電流

次へ

8.2 138 リンク・チェーン長さの計算

8.2. a   何が、138個のリンクが安定しているのを引き起こしますか?

8.2. b   テーブルA--- ドーナツチェーンの安定性

8.2. c   テーブルB--- 衝突角度

8.2. d   138個のリンクに通じる特徴

8.2. e   138個のリンクに通じる定石

戻ります。

電流

次へ

8.2. a 何が、138個のリンクが安定しているのを引き起こしますか?

どんな魔法の帽子から、我々はスペースのよりを戻しているチェーンの長さを引きましたか? 138が長い間リンクするスペースチェーンセグメントと電子チェーンセグメント137リンクはなぜ長いですか? これはddtcによって提供された最も美しい洞察の1つです。 138個のドーナツリンクのチェーンの長さはddtcに発生する数の多くを支持します。 この長さのネイチャーの選択は物理学のすべてで重要な役割を果たします。 開発がする何らかの議論がこの重要性への支払われるべきものを含んでいること。 以下の2つのグラフが長い間よりを戻しているスペースドーナツチェーンセグメント138リンクから発達する137が長い間リンクする撚り合わせているドーナツチェーンセグメントのためにはるかにすばらしい安定性を示します。 示される数は長い間表示の便利のための180個のリンクであるチェーンに制限されました。 No.最大400はテストされました。 チェーンの不安定性は、より安定したより長いチェーンにセグメントを見つけるという機会を少なくするn^2要素を含んでいます。

戻ります。

電流

次へ

8.2. b グラフA--- ドーナツチェーン親類の安定性

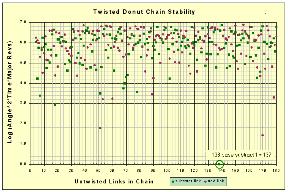視点とクリックしてください。

Aをグラフで表してください。 様々なチェーンの長さの安定性を測定します。 示される値はLog10(二乗された*時間が経過した接触調整不良角度は主循環の*番号に連絡する)です。 値は最小限である137/138値に基づいて正常にされます。

戻ります。

電流

次へ

8.2. c グラフB--- ドーナツ玉突き衝突角度

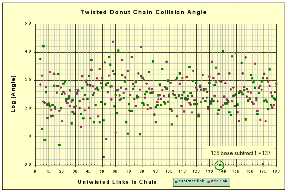視点とクリックしてください。

Bをグラフで表してください。 様々なチェーンの長さのために接触調整不良角度を測定します。 値は最小限である137/138値に基づいて正常にされます。

戻ります。

電流

次へ

8.2. d 138個のリンクに通じるドーナツの特徴

チェーン・リンク(すなわち、ドーナツの表面)の表面は本当ではありません。 唯一の本物が「ドーナツ粒子」です。 「ドーナツ粒子」は円の円の経路を旅行します。 主要な円の軸は主要なドーナツ軸です。 外側の円の軸はドーナツチューブのセンターです。 この経路は、slinkyが円を内へ曲げたように見えます。 「ドーナツ粒子」は本当の意味で存在する唯一の粒子です。 「ドーナツ粒子」の特性は物理学で他の粒子のものに混乱するべきではありません。 他の粒子はドーナツチェーンセグメントの組み合わせから発達します(中性微子以外の、それらは特定の動きを持っている結合していないドーナツ粒子です)。 ドーナツの承認のキーは存在するときドーナツ経路が安定しているという理解です。 別のドーナツ粒子をつなぐまで、事実上、基本的な「ドーナツ粒子」のどんな経路も安定しています。 そして、反対している動きは取り消されます。 次へ 正常なよりを戻しているドーナツチェーンは隣接しているドーナツのドーナツ軸とのリンクを互いに垂直にします。 接触ドーナツ粒子経路の瞬間に、少佐には軸がパイ/4の角度にあります。 この角度はその角張っている速度の小さい方のドーナツ半径倍によって分割されるその角張っている速度の主なドーナツ半径倍の接線として決定しています。 角張っている速度は相対的です。 主なドーナツ半径は主軸から内面のチューブの表面まで測定されます。 小さい方のドーナツ半径は外のチューブの半径です。 ドーナツノードの数は小さい方の角張っている速度対主な角張っている速度(すなわち、完全な革命における、未成年の外側の円の数)の比率です。 次へ ドーナツ粒子経路に適用される多くの状態があります。 我々がドーナツチェーンの幾何学と長さを測定するのを許可するのは、これらの状態です。

ドーナツリンク相互作用の安定性に影響する状態

1. 接触の瞬間の隣接しているドーナツ粒子の 速度は ほとんど同じでなければなりません。 2. 接触の瞬間の 経路指示は 密接に並ばなければなりません。 3. 接触の瞬間の 小さい方のドーナツ角張っている位置はドーナツチューブの内部に 並ばなければなりません。 4. 接触の瞬間の 主要なドーナツ角張っている位置は2つのドーナツセンターの間の 線に落ちなければなりません。 5. ドーナツ経路を横断する 時間は標準のよりを戻しているドーナツ(連動する)を横断する時間との何らかの 整数関係に堪えなければなりません。 6. ドーナツノードの好みの数には、チェーンの長さ(終わりを同期させる)の倍数があります。 7. ドーナツノードの好みの数には、(n-1)と(n+1)要素の両方があります。 上の6.からの1と小さい方のドーナツ角運動量を保存する他。 8. チェーン(エンドポイントに対する)の中の、より高い接触頻度が動揺させている影響の外で少なくなるのが好まれます。

次へ

長いドーナツチェーンは、宇宙織物創造の時間他のドーナツチェーンによってたまたま以上によって「交差されること」を持っています。 また、それらはそれらの動きにおける小変化によってさらに影響されます。 短いドーナツチェーンは第一に、別のドーナツで「リンク」であるというドーナツの、そして、より少ない機会における、より少ないノードを上がるようにします。 また、それらは受入れられる(すなわち、どこで、3つのチェーンセグメントが共通の接続で集まりますか)チェーンセグメントリンケージの角度でさらに制限されます。 これらの評価基準は、決して絶対でない、または唯一ではありません。 彼らは、ドーナツの振舞いを予測するのを助けるように思えます。 合っている条件(上の数の7.)は許容できる結果の数を大いに制限します。

戻ります。

電流

次へ

8.2. e 138個のリンクに通じる定石

2個のドーナツリンクの間の連絡先で必要で実際の経路オリエンテーション角度のdと同輩をさせてください。 nはよりを戻している正常なスペースチェーンセグメントのチェーン・リンクの数と等しくいてください。 そして、n-1リンクは撚り合わせている電子チェーンセグメントを形成します。 以下の方程式から始まってください。 必要な接触角: パイ/4d(n)=+pi/2/(n-1) 実際の接触角: (n、k)=ArcTank *(n-1)*(n+1)/ Round、[、k *(n-1)*(n+1)/ Tan、(、d(n))] 不安定性の基準: r(n、k)=、[、(n、k)-d(n)]^2 *k*(n-1)*(n+1) 当然のことnに、kを取って、k(n)に与えながら、r(n、k)を最小にしてください。 これは不安定性の基準、R(n)=r(k(n)、n)をあなたに与えるでしょう。 R(n)の値が低ければ低いほど、自由なチェーンセグメントは、より安定しています。 上式はチェーンからリンクを取り外します。 1つを加えたいならば、代理をしてください: d(n)=パイ/4--pi/2/(n+1) 次へ 状態を方程式を特定の求職者のために設計された政府仕事のための仕様に似させる方程式に置くのは可能です。 任意に特定の答えを起こす条件を出すのを避けるために、注意しました。 主な状態の議論は続きます。 138に数を狭くする最も重要な状態はa(n、k)のための表現で(n-1)*(n+1)の使用です。 nがドーナツチェーンセグメントのチェーン・リンク(ドーナツ)の数を表すドーナツモデルには、ドーナツを交替するとき、特定の関係があります。 隣接しているドーナツに連絡する前に、1個のドーナツが、ノードを持って(n-x)、(n+x)主要な革命を旅行するでしょう。 隣接しているドーナツは、ノードを持って(n+x)、連絡の前に(n-x)主要な革命を旅行するでしょう。 ノードは各革命のために主要なドーナツ軸の周りで作られたドーナツチューブの周りの回転の数(すなわち、slinkyでストランドを数える)です。 スペースドーナツチェーンは非常に密接に連動します。 この同期は、nリンクであるチェーンの各ドーナツの中のn(または、ことによると2n)ノードを長くすることによって、助けられます。 その結果、チェーン、退出の終わりにフェーズへの端に達する時までにこれはまさに相殺するそれぞれのドーナツの位置でフェーズシフトを許します。 次へ 長い間の1個のドーナツが欠けているチェーンnには、n-1ノードがあります。 これはチェーンがやむを得ずn-1を交替して、n+1ノードを採用する付属チェーンに連動しなければなりません。 また、これはドーナツの小さい方の円の動きにおける角運動量と何か同系であるものを保存します。 2番目に重要な状態は解決策のために最小にするのにおいて中古のr(n、k)に使用される表現です。 r(n、k)=、[、(n、k)-d(n)]^2 *k*(n-1)*(n+1) [(n、k)-d(n)]は衝突角度(量は実際の角度に達した完全な整列のための必要な角度と異なっている)です。 直接電磁可能性を生産するのは、この角度です。 より大きい角度は、よりすばらしい騒動を発生させます。 k*(n+1)は、接触の間のドーナツの主要な革命の数であり、ドーナツ接触の間で時間に正比例しています。 接触の間の時間が長ければ長いほど、不安定性のための機会は、より大きいです。 (n-1)はチェーンの長さよりそれほど1です。 チェーンが長ければ長いほど、構成の間、それに交差していて、接続して、有効にチェーンを2つの断片に分割して、別のチェーンがそうすることができる機会は、より多いです。 r(n、k)に置かれた状態は、道理に合うのに思えるが、このステージのモデル開発では決して当然のことではありません。 不注意に、138のチェーンの長さは強く公正に示されます。

戻ります。

電流

次へ

8.3  重力対電磁力の比率:

理論はドーナツ時間の単位あたりの接触抗力の比の合計と等しいとしてgf対efの比率を発生します。 主な電子チェーンセグメントに、これは以下と等しいです。

重力対電子/陽電子組のためのe-力の比率

a。     137   e-脚における接続 b。 x   (8.087280E-11) ^2/ 2   衝突角度のコサイン c。 x   pi^2 / 8   角度への正弦波pdf d。 /   74445^2   e-脚のドーナツ接触へのn^2 e。 /   (74445^2 + 274^2x278^2)   e-脚/スペース接触へのn^2 f。 /   (2x137x139)   スペースドーナツ接触のための要素 g。 =   2.308 E-43   2.40004E-43実験的 次へ

注意: 主な電子ドーナツチェーンセグメントだけのためにこれは重力の抗力です。 電子セグメント(それに1個のドーナツを加えて、次のセグメントから1つを引き算するのによる)の動きからの何らかの追加抗力があります。 回転している電子が旅行する経路が決定しているとき、願わくは、正確にこれについて計算することができます。 8.0872....衝突角度はドーナツチェーンでねじれに合う安定した衝突角度モードの見ることから生じます。 この数は安定しているように見えた唯一無二でした、そして、それはチェーンで例外的に均等で変なドーナツの間の正確で重要な合っている特性のボーナスで安定しているように見えました。 正弦を仮定するのからのPi^2/8結果は衝突角度の分配を振ります。 これは投機的です。 次のパラグラフで議論する要素が最終的に決定しているとき、この要素が省略されるのは、等しくありそうです。 衝突する前に(2x137x139x74445^2)は時間がドーナツ粒子に隣接して経過したマッチングによります。 この数は138ドーナツ接続チェーンセグメントとして電子チェーンセグメントのドーナツが同じ距離をいっぱいにするためにどれほど「伸びるか」に一部依存します。 この要素は得てしていくつかを変えるでしょう。 次へ (74445^2 + 274^2x278^2)は隣接しているドーナツの間の回転とrevolutionalフェーズを合わせるのによります。 この要素は、固体に見えて、衝突角度を測定するのと同じ構成から発達します。 電子回転としての撚り合わせているチェーンセグメントの強化と分解はその固まりに何かを加えます。 それはこの計算に含まれていません。 モデルで示されなかったか、または上で議論した修正は井戸へのこの数を実験誤差の範囲内に収めました。 いくつかの投機的要素がまだあるが、数と理論は上手に上げているように思えます。 示されない3つの修正は以下の通りです。 1) 衝突角度の合計は137よりむしろ普及136以上のドーナツ(ドーナツがe-脚の外に位置している状態で、チェーンの終わりのドーナツは頻繁なinterationのためほとんど修理されているように見える)です; 2) 電子と陽電子のためにわずかに異なった大衆を反映するために量を修正してあります(これは事柄/反物質の標準の視点との異なったチェーンの長さと闘争から生じます); そして 3) 変則的な磁気能率に従って、電子の固まりは実際の重力/em力の比について計算する際に減少します(この修正がいくつかによって使用されて、電子の固まりを調整して、私は、それが言及された含まれていない断片に関連するかもしれないと疑います)。

戻ります。

電流

次へ

8.4  微細構造定数の計算:

微細構造定数の計算

a。     1/137   断片、スペースによって連絡されたe-脚 b。 /   (138^2 - 2^2)   最初のスペースe-mモード c。 *   (138^2 - 3^2)   2番目のスペースe-mモード d。 =   0.00729735325   0.00729735308(33)1986CoDataに対して

調整は電磁波を運ぶ2つの補足的なドーナツ構成モードの間の変遷から来ます。 補足的なモードは隣接しているドーナツから等しい数のノードを加減させます。(そこでは、ノードの標準の数が138です)。 ノードの数はそれぞれの主要な革命のためにドーナツ重心軸の周りでドーナツチューブの周りで作られた回転数です。 異なった調整が異なった目的に1/137値に必要であったかもしれないが、値が同じくらいであったのが一般に、すべての目的に計算を使用したのが想像することができます。

戻ります。

電流

次へ

8.5  電子の大規模比への陽子:

それぞれの側へのチェーンセグメントがある三角形は陽子などの安定した粒子のありそうな候補であるように思えます。 道理に合うのに思えるそのような最も小さい候補は17個のドーナツを合計する周辺を持っています。 粒子回転は、三角形角との外部の接続が移るのに応じて側の次元が変化するのを必要とします。 次へ 料金のチェーン長さの倍の逆さの正方形の合計が二乗されたので固まりが見られるならば、三角形のための3つの外観上最も自然なステージが生産されます:

電子の大規模比への陽子

三角形側 大規模ユニット 内部の料金  外部であることの形で、加えてください:  (-1,+1,-1) ステージ1 (5+,5-,7+) 1/25 + 1/25 + 1/49 (0,0,+2) ステージ2 (5+,6,6) 1/25 (+1,0,+1) ステージ3 (6++,5-,6) 4/36 + 1/25 (+1,-1,+2) 平均   0.062451 (-1,+2,+2)/3 * 137^2   1823.96 1836.15expに対して。

追加固まりは脚の付属の料金から主なスペース織物に来ます。 この計算を終了する前に、接続の正確な絵は決定しているに違いありません。 次へ この大規模計算には問題があります。 それはe-力の比への電子重力のものより異なった計算から来るように思えます。 これは、それが間違っているのを意味することができたというわけではないか、または単に完全にまだ分かったというわけではありません。 初期の計算は、陽子、中性子、Sigma、Xi、およびオメガ粒子にはすべて、この基本的な三角形サイズがあるかもしれないのを示します(異なった料金があるいくつか)。 それは言うことができないくらい早いが、基本的なコアが同じであるならば、2^1/3と2^1/2の大規模比率は役割を果たすように見えます。 Lambda粒子がaをもっている奇人である、(、; ; 5+、5、6、5+、6、5、6++、5、6)コア三角形形。 これらの計算は、すべてかなり投機的であるが、好奇心をそそります。 2の断片的な力は、 ddtcでかなり可能に思えるが、すぐに明白な答えを提供しません。 メソンとミューオンが何であるかに関する理解はこの領域を完成するのに必要である手がかりを提供するかもしれません。

戻ります。

電流

次へ

8.6  クォーク:

離散的なドーナツの中では、クォークが単に3つのドーナツチェーンセグメントの間の関係であるというチェーン理論(ddtc)はねじれていました。別々のセグメントを持つのに必要であるセグメントの最小の数。 そういうものとして、別々の実体としてクォークについて議論するのは難しいです。 例えば、クォークの1/3の断片的な料金は、回転がある3つのドーナツチェーン側を持ちながら、陽子から生じます。 これは3つ(さらに)の異なった州からの平均した料金であるように見える料金をもたらします。 さらに、付属チェーンセグメントは各クォークのために総見かけの料金に加える変化を持っているかもしれません。 正確に電子からの深い非弾性散乱について計算してあります。 標準の計算は料金の正方形に変化します。 これは、1以来連続の1/3に請求されるように平均1、0、0が同じように働いていないのを示します。  + 0 + 0は1/9と等しくはありません。 + 1/9 + 1/9. 次へ この1つの説明が電子の構造に関するものであるかもしれません。 その回転によって、それには、料金と同様にオリエンテーションがあります。 ことによると電子電子相互作用は、これらの回転を並べさせて、完全に相互作用します。 電子陽子相互作用には、相互作用の度に影響するこのオリエンテーションの無作為の整列があるかもしれません。 これは、かなり投機的であり、精査中に召集を通過しないかもしれません。 ことによるとより良い説明は有効電荷の分配から来ることができました。 1、0、0であるよりむしろ; それは徐々にレベルを請求するかもしれません一段からの変遷が、次のステージへのレベルを宣言する。

戻ります。

電流

次へ

8.7  重力の時間の肥大:

ドーナツ衝突のための平均した仮定は大きい距離で Relativity司令官 によって生産されたそれと 等し い 重力の時間の肥大を起こします。 しかしながら、大切な区別があります。 ドーナツ衝突は離散的な過程です。 電子の直径よりはるかに大きい距離では、連続した近似は合理的です。 重力は時間の肥大を引き起こしません。  事柄は地方の「スペース時計」を遅くする交差接続です。  重力を引き起こすのは、この時間の肥大 です。 何も逃げられることができない「シュバルツシルト半径」がある純粋なブラックホールはドーナツ理論と一致しません。 そのような半径の計算を論争中にするこのわずかな規模に達するずっと前に、ドーナツスペースは離散的です。 プランク定数は1個のリンクがドーナツチェーンの周りを光速で旅行するために長い間増えた想像するドーナツチェーンでパイ/2ねじれにおけるエネルギーから生じます。

戻ります。

電流

次へ

8.8  関連性がある一貫性:

多くの読者が得てしてスペース織物がどう特殊相対性理論と一致している場合があるかに質問するでしょう。 最初に(2番目に)、一目、2が共存することができたのは無意味であるように見えます。 この共存の詳細はこの記事から省略されます。 しかしながら、運動中の物体が静止して存在した均衡としてのそのコンポーネント粒子の間の同じ電磁均衡を求めるのを除いて、直接Euclidianスペースの仮定から特別な特性なしでSpecial Relativity変化を開発することができます。 関連性のこの視点はSpecial Relativityのパラドックスに関する何らかの洞察を与えます。 結果として起こる変化は「本当」の部分と「明らかな」部分から成ります。 観察者がスペース織物に比例して静止しているならば、全体の変化は本当です。 さもなければ、それはそうではありません。 また、観測されたボディーが即座に速度を変えるならば、観察者からのその角距離は変化します。 それはパラドックスが存在しないように考えられる必要がある見かけの測定のこの不連続です。

戻ります。

電流

次へ

8.9  ドーナツサイズ:

ドーナツのスケールを測定するのは、最もややこしい問題の1つです。 プランクLengthは、サイズが結局開発したより多くの桁小さいサイズを示すように思えました。 構造がそんなに小さいのが、可能である間、すべての計算が、ドーナツサイズが137によって分割される電子の伝統的な半径と等しいのを示します。 ドーナツ粒子のサイズ、間にたぶん経路がドーナツの周りを10^-19 cm.と10^-24cmに関して旅行します。 「対称中断」を形成するために隣接しているドーナツの間の「ミス」を含む計算が得てしてこの範囲をかなり狭くするでしょう。

戻ります。

電流

次へ

9.0  Ddtc思惑

9.1   熱くAntigravity! ... 時間旅行してください。

9.2   Antigravity、あなたの望みは上がっていますか?

9.3   減速させられる時間旅行 ...

9.4   変なフリーエネルギー

戻ります。

電流

次へ

9.1  熱くAntigravity!  . . . 時間旅行してください、:

時代を通して、素晴らしい旅行では、我々のいくつがウォルターMitty*と席を共有していますか? 多分、我々は過去の競馬場を訪問しました。  . . . または、その特別な人と共に別の瞬間だらだら過ごされます。 これらの情熱は話の開きにおける悲しい章を生み出します。  時間旅行してください。  . . . 失望は我々、しかし、恐怖を消費するかもしれません。 あなたが本当に空想家としてランクを保持するならば、Mittyさんは決して死にません。 Antigravityとフリーエネルギーは未経験を誘惑します。 ドーナツ理論はこれらの動物が存在するという希望の微光を我々に提供します。 しかし、我々はそれらを利用することができますか? ほとんどのよく飼育された科学者とすべてのよく振る舞っている科学者が、フリーエネルギー(事柄の破壊のない重要なエネルギーの創造としてのI確定)が冗談であると考えます。 皮肉にも、これは未経験で通常、それほど教育されていないのに答えを発見させます。 その誤りを含んでいて、科学の教義はそれ自体のすべてに基づきます。 通常、最も活発に何かを防御するか、または否定する人々が強い偏見から行動します。 目を光らせる偏見が閉じました。 フリーエネルギーのメッセンジャーは変人のように聞こえるかもしれません。 本当に、彼らは変人でさえあるかもしれません。 彼らにそれ以上科学の教義に浸されるものほど我々の目を閉じさせないでください。  熱いAntigravityとフリーエネルギー * ジェームス・サーバーはウォルターMitty、彼の話の1つのリードキャラクタとして並はずれた空想家を作成しました。

戻ります。

電流

次へ

9.2  Antigravity、あなたの望みは上がっていますか?

反物質は経路を「反-重力」に供給するように一見したところでは思えるかもしれません。 ああ! 反物質と事柄の両方が、陽の重力を生産して、お互いを引き付けます。 彼らはそれぞれスペースの時計を遅くします。 これはドーナツ理論と一致しています。 スペースの織物からフリーエネルギーを抽出することができるならば、それは得てして、抽出されたスペースを減速させるでしょう。 物の上のスペースを減速させると、タイムワープが変化して、物は上向きに加速するでしょう。 宇宙における推進にほぼそのような高速旅行の他の困難が克服されるかもしれないと仮定する光速で「反-重力」エンジンを速度まで使用することができました。 これは、我々が他の太陽系を訪れることができたのを意味しますか? そして、彼らは我々を訪問しますか?

戻ります。

電流

次へ

9.3  減速させられる時間旅行 ...

ドーナツは多くのおもしろい経路を踊ります。 逆に、時間の退屈は限がないです。 それらのドーナツ粒子が衝突すると隣接しているドーナツがするのは、反対している動きを平均することです。 ドーナツはあなたが得ることができるのとほぼ同じくらい平均しています。 平均した過程は非常に効率が悪いです。 しかし、時間の経過が対応する変化するので、それは重要ではありません。 時間は2つの方向に旅行することができる寸法ではありません。 または、一方向に均等である、その自然な速度を除いて。 過程がどんな対応する「「非-平均」」にも処理させない平均。

戻ります。

電流

次へ

9.4  フリーエネルギー、それはKooks?に属します。

近年、スペースの織物からエネルギーを抽出することに関するますます多くの話がありました。 主に割り引かれたそうするこれがスペースと事柄の保護要件が可能であるかもしれない主な吹流し。 過程を平均する際にドーナツ織物は限のないエネルギーを「浪費します」。 我々は、ドーナツ自体の結果として起こる位置を観測して、この浪費に気付きません。 すべての時計が以前の時計に比例して遅くなったという事実は検出可能ではありません。 我々はエネルギーを抽出することができますか? それは「自由ですか?」 この質問には、どんな明答もまだありません。 ドーナツの中に利用可能な限のないエネルギーはそれが本当であるかもしれないという望みへの人の想像を可動磁石かくはんのフリーエネルギーアレンジメントのとても多くのレポートに結合しました。 時にはより冷たくなるのが助けるフリーエネルギーマシンのレポートはそれらの真実性を支持します。 ドーナツがシステムへのエネルギーを入力するパターンで衝突することができたならば、また、正反対をすることができたのはありそうに見えます。 フリーエネルギー入力/抽出は容易に検出から逃げることができました。 海洋でサーファーを考えてください。 速度を獲得しないで、サーファーは一日中上下に行くかもしれません。 技能で、サーファーはエネルギーを抽出するためにどう波に乗るかを学びます。 人類はどう「波に乗るか」を学ぶことができますか? 含意は富みます。

戻ります。

電流

次へ

主なインデックス

ページの上部

フィードバック:

作者は他のものから入力か質問に感謝します。 彼に連絡するのをためらわないでください。 あなたの利益のため、 リッシュMarkerの感謝