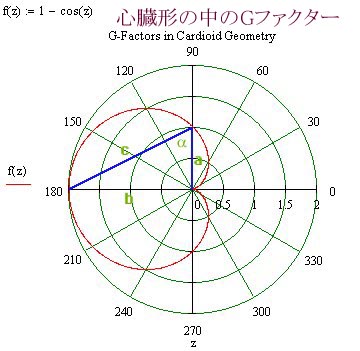
論文：物理学のための新しい基礎, by 量子エーテル力学研究所

From PESWiki

【オリハル註：細かい修正履歴⇒2006.08.02（水）08:09/08:13/08:16/11:08/11:13/11:16/15:00/15:24/16:07/22:07/22:23/2006.08.03（木）19:54/2006.08.04（金）20:10/2006.08.07（月）01:41/01:43/01:47/01:50/2006.08.07（月）18:04/18:08/2006.09.05（火）20:06】

エーテル物理学モデルはエーテル/角運動量パラダイム(アインシュタインの質量/エネルギーパラダイムと対照的に)の中で量子構造を定量化する。それは、量子力学と融合するように運命づけられており、ゼロ点エネルギーへの接続ための手段を提供する。

1 要約

5.1 量子質量
 5.2 量子電荷
 5.3 量子長
 5.4 量子周波数
 5.5 逆数的な相互関係
 5.6 基数 - 序数の関係
 5.7 序数質量という表現による重力定数の説明
 5.8 色々な量子値
 5.9 形成するための次元間相互関係

10.1 陽子と中性子の微細構造
 10.2 電荷の幾何学

11 力の法則

11.1 静電力の法則（クーロンの法則）
11.2 重力の法則
 11.3 強い力の法則
 11.4 力の担体の相対的強さ

12 その他

12.1 中性子の定量化
 12.2 中性子磁気モーメント
 12.3 g-ファクター

13 結論

14 参照

15 See also

要約

現代物理学は宇宙の機構について説明する。我々は物理学の新しい基礎を発見し、それは、高い精度と深度で宇宙の構成要素について説明する。我々はエーテルの存在、亜原子、および力の法則を定量化する。当理論のいくつかの相はスタンダード・モデルに由来しているが、多くがユニークである。

この新しい基盤からの主要なる発見は、数学的に正確な力の統一理論である。その他の基本的な発見としては、微細構造定数と亜原子g-ファクターの原点、中性子磁気モーメントのわずかな修正、電荷の幾何学構造、静電荷とは別の電磁荷の定量化、スピンというもののより正確な意味、5次元における空間共鳴の定量化、および量子単位の新しいシステムを含んでいる。

エーテルは量子の織物、すなわち電磁気、静電気、そして、重力の双極子構造を伴う回転磁界として定量化する。亜原子は、量子状に閉じ込められた角運動量、すなわち回転磁界として定量化する。すべての量子、原子、そして、分子のプロセスは正確にモデル化でき、新しい理解と洞察によって、離散的な物理学をリードすることができる。

概要

エーテル物理学モデル(APM)は量子構造のパラダイムであり、それが基づくものは、

次元というものの明確な定義、
分割された電荷次元に基づいた異なる単位系、
電子の値に基づく新しい単位系システム、
非物質的存在（エーテル）の構造、
幾何学的に評価する新しいシステム、
確立された基本定数に追加する新しい基本定数、
今まで知られていなかったタイプの電荷の定量化、
そして、角運動量としての物体の定量化。

我々は宇宙が力、物体、および環境から組み立てられていると仮定することができる。時空は「環境」の部分集合であり、それは、エーテルとして定量化される。APMの存在論は、量子物体が量子環境の中に存在しており、量子環境が量子次元の観測に作用する一次力から構成されると仮定する。一次のものとして力を仮定しよう、そして、クーロン定数とニュートンの重力定数を因数に分解する例証を挙げる。我々は、一次力を「重力定数（Gforce）」と命名し、それが一定であると仮定する、そして、そのように宇宙は閉じたシステムである。この論文では、我々は、より基本的な定数からの派生定数として重力定数を示さない。

エーテル物理学モデル（APM）は数学的であり、実証的な量子データに基づいている。現代物理学は宇宙が何をするかに焦点を合わせるが、我々は、宇宙が何であるかを定量化する。

エーテルの簡単な歴史

エーテルの概念は新しくはない。歴史的に、エーテルは後で現代物理学になったことで広く知られる理論であった。古代ギリシア人哲学者は、エーテルについて議論し、そして、数千年を通して理論は支持されてきた。1644年に、レネ・デカルトは力学的性質があり、すべてに遍満浸潤しているエーテルの哲学を提起した。「デカルトは、エーテル粒子は絶えざる運動状態にあると仮定した。しかしながら、運動粒子が動くためのどんな自由空間もなかったとき、彼は、それら自身の運動状態の中で他のエーテル粒子によって空けられた場所を得ることによって動くのだと推論した。したがって、エーテルの単一粒子の動きは、粒子の閉鎖系連鎖全体の動きに関係する；そして、これらの閉鎖系連鎖の動きは渦動を構成し、それは彼の宇宙像において重要な機能を果たした¹」エーテルについてのデカルトの概念は水槽の中で動き回る魚に比することができる。デカルト・モデルでは、エーテルは固体と液体の両方として機能する。

ホイテッカーが書き記したのは、「全空間は、若いジョン・ベルヌーイによれば、液体エーテルによって浸されており、莫大な数の極端に小さい渦を含んでいる。エーテルが持っているように見える弾性、そして振動を伝えることができる特性は、これらの渦巻の存在に本当に起因している；遠心力で各渦巻は、絶えず膨張しようとしており、そして、そのようにして隣接している渦巻に圧力を加える」²

Eisenlohrによって開発されたフレネルの公式は、エーテルが自由空間の中よりも、物質中のほうが濃密である事を指し示した³。デカルトがエーテルを完全固体と完全流体の両方であるとみなしていたが、ニコラ・テスラはエーテルが完全気体の性質を持つと推論した⁴。上記の仮説はエーテル物理学モデルの外で生まれたものである。量子エーテル・ユニットは、亜原子が存在しているところで、互いに折り重なり、そして互いに拘束し合うことができる。巨大な重力定数によって動かされるエーテルの回転磁界は、同時的に完全な固体、流体、および気体として顕われる。以下で説明されるように、エーテルに関連する質量は逆数的な質量であり、重力定数とエーテルは、これらの能力を持つ。

絶対時空としての粒子的な媒質を見つけるためにマイケルソンとモーレイが実験を行ったとき、地球が空間を通して進む事による地球を貫くエーテル流の結果として、彼らが期待したようなエーテル流に関するどんな重要な証拠も見つからなかった。しかしながら、彼らはエーテル流を測定した。デイトン・ミラーは後で、地球に対して約10,000km/sのエーテル流を確認した広範囲にわたる実験を行った⁵。もしエーテルが存在すれば、地球に対して引きずらなければならず⁶、オーガスティン・フレネルもそのように仮定した⁷通りであることをその実験は指し示した。広く行き渡っているエーテルの理解は、惑星と共に引きずられるエーテル像を容易には受け入れなかったので、エーテルの存在の証拠としてこれを数多くしつこく宣伝した。引きずられるエーテルという時期尚早な結論が、マイケルソン・モーレイの実験がどんなエーテル流も示さなかったのはその間違った仮定にあるという沢山の宣伝も行った。

さらなるエーテルの構造を推測して、Albert P. Carmenは、「我々はエーテルを無制限に多くの極微の「エーテル双極子」⁸をあるものとして考えることができると書いた。

アルバート・アインシュタインは、彼自身の時空／質量エネルギーテンソルの原理を発明し、それをエルンスト・マッハのせいにした。彼は、時空は質量に作用し、そして質量は時空に作用すると原則的に述べた。しかしながら、アインシュタインの見方が、経年を通じて複数回変化したのは、彼の一般相対性理論に基づいた、物理学に対する正確な指摘をする能力の欠如に起因する。結果としては、アインシュタインの初期の間違った考え方で、一般相対性理論に関する矛盾が為に、アインシュタインはこれらのアイデアと結局は縁を切ったにも関わらず^9、10、今日の正確な物理学概念（マッハの原理、宇宙定数）として現存している。

アルバート・アインシュタインはエーテルの存在の反証をしなかったし、論駁する試みもしなかった。1920年5月5日にLeyden大学で、アインシュタインは講義を行い¹¹その中で彼は自身の趣向にも関わらずエーテルの存在を擁護した。アインシュタインの理論が物理学にある絶対時空間へのいくつかの参照を強く維持することに基づいたので、彼は彼の時代のエーテル議論のトップに位置しなければならなかった。Robert ShanklandによるMillerの研究の再調査では、Dayton Millerの研究に対してアインシュタインは自身の死後に弱体化させるように圧力をかけることとなり、そして、ShanklandはMillerの測定したエーテル流は装置の中の温度異常¹²であるとして書き下ろそうとした。

APMは、エーテルの初期の概念をしっかりと定量化し、堅実な基礎をアインシュタインの一般相対性理論に提供するが、彼の特殊相対性理論はサポートしない。

ゴールと目的

APMは、物理学の全ての側面について説明する能力がある。しかしながら、当理論は広範囲であり、かつ、紙面は限定的であるため、我々はこの理論のいくつかの本質的基礎を提示するつもりである。いくつかの概念は発表の中で包括的には見えないかもしれない；しかしながら、我々の本、エーテルの秘密Secrets of the Aether (http://www.16pi2.com/book.htm)¹³ではさらにAPMを展開している。

重力定数はエーテルの原因として定量化する。エーテルは、物体が存在するための非物質環境として順番に定量化する。量子環境を理解するには、量子物質がどのように動くか、そして、重力定数が静電気、電磁気、そして、重力をどのように発生させるかを理解することが不可欠である。このエーテルの新しい理解から、APMは数学的に正しい統一理論を提案し、そのようにして、簡単に数学的法則ですべての力を統一するのに成功した。

定義 - 次元

ここで定義される次元Aは、非物質であり、存在の基礎に関連する測定可能な特質である。以下に示された定義はエーテル物理学モデルの基礎に必要不可欠である。当定義は実証的なデータを批判的に分析することによって決定したので、方程式はデータを表現するようになった。それら以下に示した詳細を超えた分に関しては、エーテルの秘密¹³を見て下さい。

量子質量

「質量エネルギーの等価性」の概念と、「余剰質量」¹⁴の概念はAPMでは意味を持たない。次元というものは単位の構成要素であり、単位そのものではない。この理論では、次元としての質量は、単位としてのエネルギーよりも違う現実の階層を持つ。質量に数量が与えられると、慣性の寸法になることを、次元としての質量と定義しよう。この理論における、質量の初期量は電子の質量（m_e）である（キログラムまたはグラムに反対する）。電子を除いて、その他の振る舞いを分析する時に質量数量を使用する必要性がもしあるならば、我々は単に陽子の質量をm_p、中性子の質量をm_n、およびエーテルに関連した質量をm_aとして参照する。質量は直接的に観測できないが、単位の中の質量次元の整理から属性を推論することができる。質量は単位の中の1つの次元として通常現れるので、質量次元の幾何学は本質的に線形であると仮定しよう。量子レベルの環境が曲線なので、質量の線形の本質も同様に曲線であると推論するつもりである。質量の次元を長さの次元に掛けるとき、それは我々がligamen circulatus（LC）¹⁶と呼ぶ量子構造を作り出す。質量の円形ストリングとして(LC)を考える。

量子電荷

電荷を次元と定義しよう、数値が与えられると、電気の寸法になる。電荷には静電荷と電磁荷の2つの表現がある。標準理論では、電磁荷は静電気の相対論的表現として定量化する。APMでは、電磁荷はクーロンの二乗の次元と共に簡単なニュートンの型式の表現を使って定量化する。

観測から、我々は、電荷が表面を覆う時、電荷間にはどんな間隙もないことがわかる。電荷が分割された長さ（面積）の上に存在しているので、電荷次元も分割されると仮定しよう。APMでは、その量子静電荷は、確立された理論における素電荷と同じ値であり、その次元を除いて、分配された電荷を表現するように修正する。したがって、我々はe²として量子静電荷を記述する。また、Charles Coulombは、電荷の分割を提案した¹⁷。

第二の種類の電荷があり、電磁荷と名づけられており、すなわち強い電荷は、電子についてe_emax²、陽子についてはe_pmax²、中性子についてはe_nmax²、およびエーテルについてはe_a²と記述される。強い電荷は、エーテル伝導率に対して亜原子の角運動量倍として定量化し、そして、静電荷とは異なった幾何学としての定量化可能性を持っており、後で当論文で説明される。すべての電荷は分割されるが、単位の中の電荷の次元と共に、分割された長さの次元が明確に表われない場合、この幾何学に関連するどんな長さも存在しない。(例えば、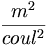 $\frac{m^2}{coul^2}$ ).

電荷の次元は、電子または陽子と同じではない。したがって、エーテル物理学モデルでは、大量の電荷が、与えられた空間容積の中に存在すると言うことができない。電子と陽子が分割された電荷を持ち、電子と陽子が与えられた空間容積の中に存在するという言いかたは正しいだろう。

量子長

長さを次元と定義しよう、数値が与えられると、距離の寸法になる。APMにユニークな量子測定分析と呼ばれるテクニックを適用することによって、我々は、コンプトン波長が宇宙全体が組み立てられる量子の長さであると決定することができる。我々はプランク定数の特定のケースを取り上げるつもりである;しかしながら、このテクニックはすべての量子定数に適用される。プランクの定数は次のように計算される：

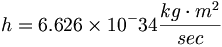$h=6.626\times10^-34\frac{kg\cdot m^2}{sec}$ (5.1)

Max Planck¹⁸によると、この定数は「作用の量子」である。量子レベル(電子、陽子、そして中性子)で「作用する」ことができるのは3つの亜原子だけであり、3つの中で電子が最も動き易いので、作用の量子を直接、電子と仮定して言及しよう。したがって、我々は、質量次元が電子の質量を表すと推論することができる。ここで3つの次元が残っており、内2つの速度の単位を作り出す。量子速度が光速であると仮定しよう。これは剰余を残す：

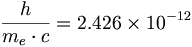$\frac{h}{m_e\cdot c}=2.426\times10^{-12}$ (5.2)

これはコンプトン波長と等しい。

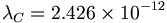$\lambda_C=2.426\times10^{-12}$ (5.3)

したがって、量子長をコンプトン波長と定義して、 $λ C$ として記述しよう。

量子周波数

周波数を次元と定義しよう、数値が与えられると、時間間隔の寸法になる。通常、我々は時間の次元の中で考える。それにもかかわらず、我々の時間計測装置のすべてが直接周波数として測定する。APMでは周波数は、単位表現の分母の中に現われた時間次元によって根拠付けられる、通常に表現された次元である。基数と、序数の値の次元を扱うのに慣れてくると、通常の次元としての周波数をより良く理解できる。量子測定分析の方法を使用して、我々は光速を量子長で割った商として量子周波数を定義し、 $F q$ と記述する。

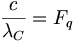$\frac{c}{\lambda_C}=F_q$ (5.4)

逆数的な相互関係

すべての次元には、表面上の、そして、逆数的な特性がある。曲折または周期的であるところの、平面または線形であり逆数的である表の次元を考えることができる。一般に、その逆数的な次元は逆数単位あたりの表の周期として読む。例えば、時間は表の次元であり、線形性を持ち、一方、その逆数の時には、時間当たりの周期である。同じ論理は長さ(線形である)の表面次元とその波数(単位長さあたりの周期)の逆数に適用される。

質量にもまた、逆数的な相がある。我々は逆数的な質量を、正と負に周期的に交換する慣性として考えることができる。往復ピストンは、行ったり来たりする長さの次元に沿って慣性を循環させる。しかしながら、エーテルと重力定数では、エーテルの質量は行ったり来たりする時間の次元（または周波数の次元）に沿って慣性を循環させる。そのエーテルは質量に関連した巨大な逆数質量を持つのだが、その総慣性はゼロとして現れる。

また、逆数質量は重力定数の中にも現われる。APMでは、電子質量は角運動量という量子的振る舞いと離れて存在することはできない。APMでは、この運動の量子を一次角運動量と呼び、そして存在の特殊な形式と看做す¹⁹。さらに、一次角運動量は、エーテルの中に存在せず、暗黒物質(現代の宇宙物理学で広く使用される意味で)と命名する。暗黒物質が量子エーテル・ユニットに吸収されるとき、そのエーテルは一次角運動量に対して、電荷の色々な性質を伝達する、そして、その結果、それは目に見える物体(そして、反物質)になる。

ここで仮定しようと思うのは、一次角運動量が時間の順方向でだけスピンすることができるということで、このようにして、エーテルの慣性が時間の順方向と逆方向の間を振動するとき、一次角運動量は半サイクル進むだけであるとする。したがって、一次角運動量は半スピンである^{20、 21}。重力定数が一次角運動量の中で質量次元に作用すると、押す力か引く力のどちらかを出すことができると仮定する、ただ両方同時はない。重力定数が質量次元に関して押す力、引く力のどちらを出すかは、亜原子のスピン・パリティであるように見える。したがって、物質は物質を引き付け、そして、反物質は反物質に引き付けるだろうが、物質は反物質を退けるだろう。

電荷は誤解されている次元である。電流は、電荷が表面的に広範囲に使用されている唯一の単位である。電流の単位では、電荷は線形の量である。しかしながら、電荷は通常、他の単位の分母に、そしてその逆数の形として現れる。逆数的な形では、我々は単位電荷あたりの周期であると読む。例えば、電位は、単位電荷あたりのエネルギー単位である。磁束は、単位電荷あたりの角運動量である。抵抗は、単位電荷あたりの磁束である、と、このようになっている。

SMでは、1種類の電荷量子、素電荷だけがある。強い力を定量化する試みで、以前の理論では、グルオンとパイオンの存在を仮定し、そのカラーとフレーバーという言葉の中で電荷を定義した。²¹それ自体、単位電荷あたりの角運動量の概念なのだが、以前の理論の理解の中では無意味に聞こえる。しかしながら、APMでは2種類の量子電荷があるのだが、素電荷は2つの中では比較的重要ではない。電磁荷は、磁気モーメントを除いて、すべての電荷の中で参照される関連単位としての電荷である。磁気モーメントの場合は、単位は両種類の電荷を参照する。この論文の第12章で説明される。単位は一般的に、静電荷ではなく電磁荷を参照する。以前の理論は静電荷に関連してそれぞれの亜原子の電磁荷を定量化していない。これが、以前の理論では、力を統一することが出来ない理由である。

基数 - 序数の関係

我々は、APMで物理学表現における分子が、数学的に基数値(数量)を持っている傾向があると仮定し、そして、分母は数学的に序数値(位置)を持っている傾向がある。物理学的見地から、我々は、絶対次元として分子を特定して、相対的な次元として分母を特定することができた。乗法は基数と評価された絶対次元の間で行われる。そして、序数と評価された相対次元の間で行われる。しかしながら、基数と評価された絶対次元は、序数と評価された相対次元によって割り算され、逆もまた然りである。絶対数量は客観性に一致しているが、相対位置は主観性、または、環境に関係している。

質量は、基数であると評価された次元であり、質量の逆数は序数であると評価された次元である。その結果、重力定数とエーテルは質量の逆数から導かれ、このようにして、それらは我々が慣れ親しんでいる質量の物理的な表現（基数、または絶対値）とは対照的に、序数的または相対的である。

多くの場合、電荷は逆数次元である。それが表の次元(電流の単位中に、のように)に現れたとき、その電荷は客観的な数量である。しかしながら、電荷は、たいていは序数として現れ、その結果、主観的な環境で適用される。

我々は、基数としての質量と電荷を客観的実在と関連していると考えることができ、一方、序数としての質量と電荷は環境的、または、主観的な現実に関連されると考えることができる。環境は非物質的であるが、環境の定量化は、実在的な物体の定量化の理解と同じくらい不可欠である。

序数質量という表現による重力定数の説明

APMで重力定数を導く：²²

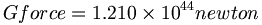$Gforce=1.210\times10^{44}newton$ (5.5)

2つの測定質量は、エーテルに関係した質量の総量に等しいことについて考える。ニュートン重力定数については、妥当な精度に決定された²³のだが、これらの質量は互いにある量子長の距離を隔てているとしてみる。それらの間には結果として起こる力があるだろう。

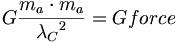$G\frac{m_a\cdot m_a}{{\lambda_C}^2}=Gforce$ (5.6)

我々は、重力定数が環境的、または主観的であるという事がわかるようになりつつある。

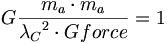$G\frac{m_a\cdot m_a}{{\lambda_C}^2\cdot Gforce}=1$ (5.7)

APMでは次のようにエーテル・ユニット値が導かれる：

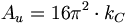$A_u=16\pi^2\cdot k_C$ (5.8)

これは、エーテル電磁定数と、クーロンの静電定数である。もし我々が2つの電荷の観測値を取り、それがエーテル(以下の量子値を見よ)の強い電荷に等しいとしたら、ただ1つの量子長でそれらは離れている：

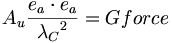$A_u\frac{e_a\cdot e_a}{{\lambda_C}^2}=Gforce$ (5.9)

つまり、環境的な重力定数も、強い電荷の観測値の逆数である：

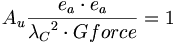$A_u\frac{e_a\cdot e_a}{{\lambda_C}^2\cdot Gforce}=1$ (5.10)

（分配型電荷が増えるとき、経験上、それぞれの分配型電荷のただ一つの次元だけが使用される）

色々な量子値

量子測定値

表 1
名称	シンボル	値
電子の質量	m_e	9.109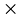 $\times$ 10^-31 kg　　²⁵
陽子の質量	m_p	1.673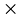 $\times$ 10^-27 kg　　²⁶
中性子の質量	m_n	1.675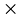 $\times$ 10^-27 kg　　²⁷
エーテルの質量	m_a	3.268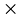 $\times$ 10¹⁵ kg　　²⁸
静電荷	e²	2.567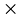 $\times$ 10^-38 coul²　　²⁹
電子の強い電荷	e_emax²	1.400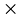 $\times$ 10^-37 coul²
陽子の強い電荷	e_pmax²	2.570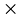 $\times$ 10^-34 coul²
中性子の強い電荷	e_nmax²	2.573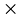 $\times$ 10^-34 coul²
エーテルの強い電荷	e_a²	5.021 $\times$ 10⁸ coul²
量子長	$λ$ _C	2.426 $\times$ 10^-12 m　　³⁰
量子周波数	F_q	1.236 $\times$ 10²⁰ Hz

形成するための次元間相互関係

図 1

長さと周波数の次元が結合して幾何構造を打ち立てると仮定する。一方、質量と電荷の次元は物質を打ち立てる。幾何学的、そして、物質次元は特定の幾何学的定数に関連する。エーテル・ユニットの中での共鳴のため、そのエーテルは幾何構造を曲がらせた。エーテルの中の曲がった幾何構造それ自体が、次元の本質を帯びる。

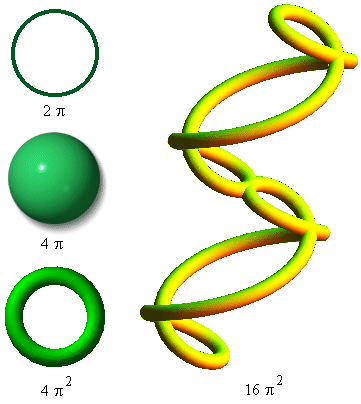
エーテルの中に幾何構造の連鎖がある。その単位全体にわたる単次元としてその質量が現れるのを観測するにつれ、我々は質量は線形性を持っていると仮定する事が出来る。円は曲がっている線形構造なので、質量と幾何学的な定数2πを相互に関連付けよう。

さらに、APMでは電荷は分布しているものと定義されるので、我々は電荷には表面的性質があると仮定することができる。エーテル・ユニットの中での共鳴は2つの球を作り出す。それはまた、我々が、静電荷と呼ぶことができる一種の静的な周波数と互いに関連するのを観測する。静電荷のこの静的な周波数の値は素電荷の源である。そのようにして、静電荷が球体であり、4πの幾何学的な定数を持っていると仮定しよう。

我々がAPMで分かった事は、電磁荷がエーテルの伝導率（伝導性）の角運動量倍に等しいことである。

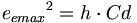${e_{emax}}^2=h\cdot Cd$ (5.11)

我々は、より大きな円の中で垂直に動く、質量の円形ストリング(LC)としてその角運動量モデルを見出すつもりである。トロイドは、より大きい円に沿って移動する小円であるので、電磁荷はトロイドに関連しており、4π²の幾何学的な定数を持っていると仮定しよう。

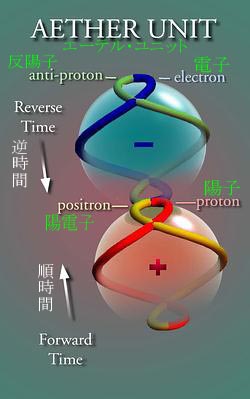
その定数16π²は、二乗された球の定数に等しい。図1に見られるように、そのエーテル・ユニットは4つの順時間スピン位置³²が存在する二重航程線³¹を超えて2つの直交した球であると仮定される。4つのスピン位置のそれぞれが1つの亜原子に対応するだろう。亜原子がその角運動量と等しく、そのエーテル・ユニットの中でスピンするその一次角運動量がトロイダル状の強い電荷を発生するので、その時、その4つのスピン位置に、16π²の幾何学的エーテル定数を発生する目的のために4π²のトロイダル状定数を掛ける。

このようにして、我々は幾何学的定数の発展を見ることができる。

図 2

経験的に我々が見出したのは、電磁定数(A_u)が、時間に影響されたトロイダル、あるいは、より正確に言えば、一つの心臓形³³に属し、そして、静電定数(k_C)が球形³⁴に属することである。方程式4.8から我々は、クーロン定数が立体角1とエーテル・ユニットを証明することができると仮定することで、立体角16π²　³⁵を証明することができる。cgs単位系の中に含まれる電磁定数と、そして、静電定数を見るとき、このことが反映している：

k C = 1

(5.12)

A u = 16π 2

(5.13)

方程式5.14で見られるように、エーテルは周波数の2つの次元と直交した長さの次元の計3つの次元で構成される。

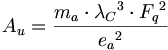$A_u=\frac{m_a\cdot {\lambda_C}^3\cdot {F_q}^2 }{{e_a}^2}$ (5.14)

長さの3つの次元については、長さの2つの次元は二重航程線の表面に起こり、長さの1つの次元はエーテル・ユニットの間に起こる。周波数の2つの次元は、2つの球へ起こり、共鳴単位を生成する。古典物理学によると、二乗された周波数は、共鳴に等しい。

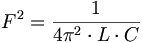$F^2=\frac{1}{4\pi^2\cdot L\cdot C}$ (5.15)

古典物理学は、共鳴周波数を共鳴の平方根であるとみなす。しかしながら、我々は、共鳴の直接測定がフーリエ変換の必要性を無くすと予測することができる。というのは、正しい次元の形としてそのデータが既に存在するだろうから。

エーテルには5つの空間-時間の次元が与えられる点に注意せよ。体積として現れる長さの三次元がある、そして、共鳴として現れる周波数の2次元がある。したがって、エーテル・ユニットは4次元的空間-時間とは反対に、5次元的空間-共鳴として実際に存在している。

本来周波数は分割された次元であって、絶えずその方向を取り替えるので、その結果、カーブを生成する。二乗された周波数、または共鳴は、2つの直交した曲線であり、その直交曲線は三次元曲面に帰することができる。この三次元曲面は長さの次元を含まないが、それは二重航程線の曲線構造を導く。簡単に、共鳴は時間-空間の中での曲率の原因である。共鳴の二重球は、その2スピンの性質³⁶と関連してエーテルの中に現れる。

忘れないで下さい、重力定数に関連した質量は、往復動している慣性である。重力定数は、エーテルの強い電荷単位で二乗される長さの量子次元に作用することによって、二重航程線構造と共鳴の両方をもたらす。

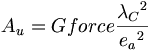$A_u=Gforce\frac{{\lambda_C}^2}{{e_a}^2}$ (5.16)
共鳴は時間の順方向に生起する。時間には順方向と逆方向があり、それに伴い、重力定数の往復慣性が振動している。

エーテル・ユニットは4つの離散的な【相互独立的に分離した】スピン位置で構成される。2つの陽性スピン位置(陽電子と陽子)と2つの陰性スピン位置(電子と反陽子)がある。電子と陽子は共に左手スピンである、そして、陽電子と反陽子は右手スピンである。これは、Tsung Dao LeeとChen Ning Yang.³⁷によって進展したスピンパリティ理論に違反することに同意する。これらのエーテルスピン位置は、それらに固有の物理的実体を持っていないが、その中で亜原子が存在することができる空間-共鳴を提供する。

要するに、量子周波数には3つの軸がある。量子周波数の最初の軸は、順そして逆時間である。量子周波数の2番目の軸は、右手そして左手スピンである。これら最初の2つの量子周波数の軸が動的である。量子周波数の3番目の軸は、静的であり、正負静電荷である。

エーテルの幾何学

我々の空間-時間の認識は量子エーテル・ユニットから生じる。それは、量子的な回転磁場である。エーテル・ユニットは、強い電荷あたりの面積の次元に関して作用している重力定数から構成される。重力定数には、先立つ原因があるかもしれない。強い電荷は単一性の中での分裂から生起した。しかしながら、重力定数の起源も、単一性の中での分裂機構の背景も、この論文に相応しい題材ではない。当分、我々は物理的存在の機構から、この新しい物理学の基礎を確立しなければならない。

重力定数は、加減速しているエーテル質量である。エーテル慣性が正の方向に動き、そして逆方向に動くに従って、それは、共鳴の各方向では加減速する。重力定数は以下に等しい：

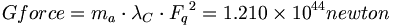$Gforce=m_a\cdot \lambda_C\cdot {F_q}^2=1.210\times 10^{44}newton$ (6.1)

重力定数は、エーテルの「ストローク」という強い電荷あたりの表面に影響することによって、エーテルをもたらす。

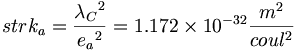$strk_a=\frac{{\lambda_C}^2}{{e_a}^2}=1.172\times 10^{-32}\frac{m^2}{coul^2}$ (6.2)

以前に言及したように、宇宙は3つの本質から構成される。力、環境、および物体。エーテル・ユニットはその時、力に含まれる。

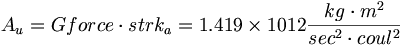$A_u=Gforce\cdot strk_a=1.419\times 10{12}\frac{kg\cdot m^2}{sec^2\cdot coul^2}$ (6.3)

エーテル・ユニットは、その中に物体が存在する環境であり、また、クーロン定数の16π²倍に等しい：

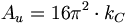$A_u=16\pi^2\cdot k_C$ (6.4)

また、エーテルは物体の中に表現される。我々は電子に固有の場合を考えるつもりである。しかしまた、陽子と中性子に関しても考える。

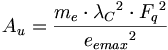$A_u=\frac{m_e\cdot {\lambda_C}^2\cdot {F_q}^2}{{e_{emax}}^2}$ (6.5)

本質的には、宇宙は回転磁界【オリハル註：渦動、渦流】の中に存在している。量子について理解するために、マクロ、または、宇宙レベルの存在について、回転磁界の徹底的な理解を必要とするように思えるだろう。そのような次第でAPMはHannes Alfven³⁸によって最初に提唱されたプラズマ宇宙論を強く支持するものである。

クーロン定数はさらに4つの定数－光速、エーテルの伝導率、エーテルの透磁率、およびエーテルの誘電率－から構成される。

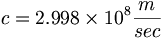$c=2.998\times 10^8\frac{m}{sec}$ (6.6)
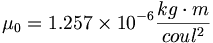$\mu_0=1.257\times 10^{-6}\frac{kg\cdot m}{coul^2}$ (6.7)
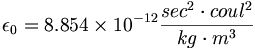$\epsilon_0=8.854\times 10^{-12}\frac{sec^2\cdot coul^2}{kg\cdot m^3}$ (6.8)

当分エーテルの重要な伝導率定数を以下であると定義しよう。

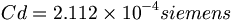$Cd=2.112\times 10^{-4}siemens$ (6.9)

上の定数へのクーロン定数の関係は以下の通りである：

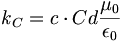$k_C=c\cdot Cd\frac{\mu_0}{\epsilon_0}$ (6.10)

エーテル双極子

電子の角運動量はプランク定数(h)である。我々は、陽子と中性子の角運動量を、それぞれh_pそしてとh_nと記すことができる。次に、陽子と中性子の角運動量の構造が電子と同様の構造に従うと仮定しよう：

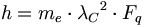$h=m_e\cdot {\lambda_C}^2\cdot F_q$ (6.11)
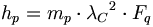$h_p=m_p\cdot {\lambda_C}^2\cdot F_q$ (6.12)
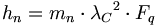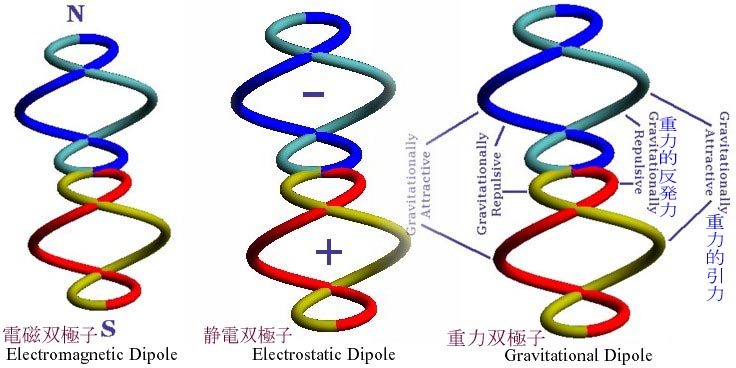
$h_n=m_n\cdot {\lambda_C}^2\cdot F_q$ (6.13)

Albert Carmenが仮定したように⁸、量子エーテル・ユニットは双極子構造である。我々は、3種類の双極子を示すことができる：電磁気、静電気、および重力である。図3は、エーテル・ユニットとその双極子について描いた3つの図解である。

図3
双極子構造

電磁双極子は電磁気の(強い)電荷に適用される。強い電荷値は、亜原子粒子の角運動量倍のエーテル伝導率に等しい：

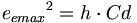${e_{emax}}^2=h\cdot Cd$ (6.14)
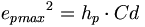${e_{pmax}}^2=h_p\cdot Cd$ (6.15)
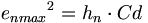${e_{nmax}}^2=h_n\cdot Cd$ (6.16)

静電双極子は、エーテルの静電気的量子周波数次元が寄与し、それは単にe²である。静電荷は単一性の中の分裂で生じたが、今のところ静電荷は基本的であり、量子周波数であると仮定しよう。

重力双極子は亜原子粒子の角運動量のスピンパリティに相当する。類似のスピンパリティに付随する角運動量群は、重力的引力であり、反対のスピンパリティ群は重力的反発力である。したがって、物質は反物質に対して重力的に反発する。

重力的反発

APMでは、中性子とは拘束された電子と陽子であり、中性の静電荷³⁹の結果である。それにもかかわらず、中性子が崩壊した時の、電子と陽子はそれぞれの固有の静電荷を保持することがわかる。同様に、単電子の質量として定義される光子の角運動量は、エーテル・ユニット⁴⁰の中にある電子と陽子のスピン位置に分割される。APMでは、陽子を、総角運動量の光速倍として定量化する。

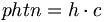$phtn=h\cdot c$ (7.1)

光子の持つ総質量が一つの電子のものに等しいのだが、質量は物質と反物質に等分割されるので、質量は重力的に互いに無効化される故に、質量の無い光子が出現する。にもかかわらず、原子が光子を吸収するとき、光子の角運動量群は一体化することができ、そして総質量と共に、個々の電子と陽電子を生成できる。これらの現象は光電効果、コンプトン効果、および電子対生成として理解されている。

吸収された光子がどれほどの電子と陽電子を放射することができるかをデモンストレーションする一つのデバイスがある。我々は、デバイスをCrookeの放射計と呼ぶ。光子が吸収されると、電子を羽根の暗い側面から放射し、そして、陽電子を羽根の鏡面から放射する。電荷は物体、反物質の無効化のためガラス球内に蓄積しない。物体、反物質が無効化する前に、放たれた電子と陽電子は羽根に力を伝達する。電子と陽電子の無効化で、より多くの光子を発生する。いくつかの発生した光子が羽根の方向に戻って、当プロセスを繰り返す。加熱された分子の標準的な説明は、ガラス管内の温度増加を実証しない。羽根の近辺の空気分子群の急速な加熱と冷却は、明るい日光で達成される急速な回転に関する説明としては考え難い。

したがって、羽根の表面に作用する光子との関係は以下に等しい：

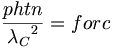$\frac{phtn}{{\lambda_C}^2}=forc$ (7.2)

方程式7.2でphtnとforcは、Aether Physics Modelによって定義される量子測定単位である。真の量子光子の単位はphtnであり、そして、力の量子測定単位はforcである。forcの単位は0.034ニュートンに等しい。

APMは量子測定単位の完全な新しい一つのシステムを含んでいる。量子測定単位のすべてが4文字略語として表記される。量子測定単位が既に定義されていた（hは角運動量の量子測定単位であり、cは速度の量子測定単位である）ところを除いて。

電荷、電磁気、そして、静電気

量子電荷の定義で示したように、異なった2種類の電荷の顕現がある。実験的な素電荷は、静電荷のAPM量子を定義する。

電磁荷はまた、強い力を司る為に強い電荷と呼ばれ、それはエーテル伝導率に亜原子粒子の角運動量倍したものから得られる。電子の作用量子についての量子測定分析に基づけば、プランク定数は次のものに等しい：

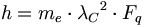$h=m_e\cdot {\lambda_C}^2\cdot F_q$ (8.1)

方程式6.11～6.13に従って、すべての亜原子の総角運動量を定義しよう。

方程式6.4と6.10が示すように、クーロンの静電気定数と言われているエーテル・ユニットの構造は、光速、エーテル伝導率、エーテル透磁率、およびエーテル誘電率から構成されると仮定する。

そのため、我々は電磁荷を、エーテルの伝導率定数に、亜原子の角運動量を掛けたものに等しいものとして、方程式6.14～6.16のように定量化することができる。各亜原子粒子には、そのようにして、ユニークだが一定の電磁荷があり、それは亜原子の質量に正比例している。

物質

定量化

質量は線形なので、物体との関連では、長さの単なる一次元として存在している。亜原子レベルの物質は一次角運動量として存在している。一次角運動量は、円に対して垂直に回転している速度である質量（環状拘束力）の環状線に等しい。その電子の角運動量は、プランク定数⁴¹としても知られている「作用の量子」である。

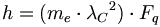$h=(m_e\cdot {\lambda_C}^2)\cdot F_q$ (9.1)

プランク定数が作用の量子であるので、それは電子を直接に定量化している。プランク定数は電子である。プランク定数周辺の事象が明確である故、我々は、亜原子粒子群が一次角運動量の単位ではありえないと勝手に決定付けるべきではない。

類似の構造は陽子と中性子にも適用される。同様に、亜原子粒子の質量は、その角運動量と不可分である。このように、一つの亜原子粒子の質量が与えられているとき、我々はその角運動量を予想することができ、そして同様に、角運動量が与えられているとき、その質量を予想することができる。

ある速度で動いている質量の円として存在する電子は、電子スピン位置であるエーテルの内部構造に合致する。角運動量には、各亜原子粒子と同じ構造があり、それぞれの亜原子粒子にユニークなスピン位置が満ちている。亜原子粒子の概念がAPMでは従前の理論よりいくらか異なっているので、Henry Margenauの提案によって、我々はそれらをonn(ontaの複数形)⁴²と命名する。

暗黒物質

暗黒物質を一次角運動量とみなすと、それは、量子エーテル・ユニットの電荷機構の外部に存する。経験的に、目に見える物体とは作用しない暗黒物質の広大な海がある。重力作用を除いて。この理由は、一次角運動量には、固有の強い電荷または静電荷がないからである。一次角運動量が吸収されたとき、エーテル・ユニットはこれらの2種類の電荷特性を伝達する。

暗黒物質は、カシミール効果⁴³を通じて光子の発生によってエーテルの中に吸収される。ある距離を隔てた2枚の金属板AとLの間に働くカシミール引力を計算している方程式を以下に示した。我々は、量子測定分析の目的のための量子距離になるように、その長さと面積を選ぶ。

L = λ C

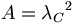
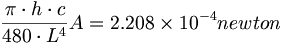: $A={\lambda_C}^2$ $\frac{\pi\cdot h\cdot c}{480\cdot L^4}A=2.208\times 10^{-4}newton$ (9.2)

オランダ人の物理学者ヘンドリック・カシミールは1948年に方程式9.2を打ち立てた。1996年にSteven Lamoreauxがカシミール効果の方程式を5%まで確かめた実験を行った。⁴⁴

方程式9.2を見ると、我々は分子の中にこれ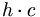 $h\cdot c$ があることが分かる。エーテル物理学モデルでは、それ 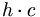$h\cdot c$ は量子光子の単位に等しい。APMの立場から、その方程式の 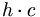$h\cdot c$ をphtn単位に置き換え、forc単位系で力を表現してみよう。

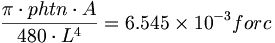$\frac{\pi\cdot phtn\cdot A}{480\cdot L^4}=6.545\times 10^{-3}forc$ (9.3)

我々が量子距離にL、量子距離の二乗にAを選んだので、その数値項は独自性を持つ。

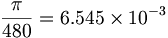$\frac{\pi}{480}=6.545\times 10^{-3}$ (9.4)

480によって割られた数値項πが、無視することができないくらい1/16π²の近くにある。(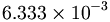 $6.333\times 10^{-3}$ )それはカシミール方程式が不当に計算されたり、あるいは推論されたということだろうか？恐らく、それは以下の通りであるべきである：

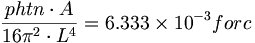$\frac{phtn\cdot A}{16\pi^2 \cdot L^4}=6.333\times 10^{-3}forc$ (9.5)

仮定された数値項16π²に対する元のカシミール方程式における、その数値項の比較により：

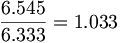$\frac{6.545}{6.333}=1.033$ (9.6)

カシミール値は、16π²より、丁度3.3%大きい。1996年に、Steven Lamoreauxはカシミール効果を実計測し、カシミール方程式に含まれる5%までを測定した。それ故に、想定された値16π²は正しいかもしれない。一層興味深いのは、phtn/16π²が「クーロン定数」の「電子の強い電荷」倍に等しいということである。

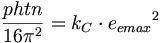$\frac{phtn}{16\pi^2}=k_C\cdot {e_{emax}}^2$ (9.7)

我々は、いわゆる「仮想光子」が強い力によって作用を受けた電子の強い電荷の結果としてカシミール効果で生成されるのがわかる。したがって、カシミール方程式は以下のように変換できる：

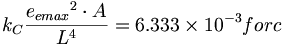$k_C\frac{{e_{emax}}^2\cdot A}{L^4}=6.333\times 10^{-3}forc$ (9.8)

ゆえに、カシミール効果は、クーロン法則の形を取りつつ互いに引き合う金属板の中の原子の強い電荷である電子の結果であるように見える。しかしながら、Lamoreauxは彼の論文、「There was no evidence for a force in any of the data….（どのようなデータにも力の証拠が存在しなかった）」⁴⁴で明確に述べている。それにもかかわらず、その力は、力の逆二乗ではないが、彼が「カシミール力は非線形であり、0.5μm未満の距離で急速に強まる」と書いているように、距離が近くなるにつれて、急速に増加する。これは逆二乗の法則に従って増加する強い力の法則と完全に一致しているが、静電気力よりも16π²倍鋭い率で強くなる。

量子長になるように長さと面積を取り、調整されたカシミール方程式は、電子用のAPMでの強い力の方程式として以下のように変換し、簡素化する。

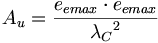$A_u=\frac{e_{emax}\cdot e_{emax}}{{\lambda_C}^2}$ (9.9)

したがって、カシミール効果の実験の成功は、電子の強い力の法則と同様、電子の強い電荷の存在証拠である。また、それは、「光子」が「光速」の「電子の角運動量」倍に等しいという主張をサポートするための証拠を提供する。

力の相互作用

静電気と、強い電荷を定量化したので、我々は弱い相互作用を定量化することができる。強い電荷に対する静電荷の割合は、onnの微細構造の8π倍に等しい。

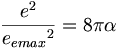$\frac{e^2}{{e_{emax}}^2}=8\pi\alpha$ (10.1)

陽子と中性子の微細構造

物理学の標準モデルは陽子と中性子のユニークな微細構造を充分には認めていない。しかしながら、我々はすべてのontaが同様の構造を共有するという仮定に基づく陽子微細構造と中性子微細構造について計算することができる。方程式9.1の構造に基づいて、我々は陽子と中性子の微細構造について計算することができる。

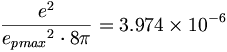$\frac{e^2}{{e_{pmax}}^2\cdot 8\pi}=3.974\times 10^{-6}$ (10.2) 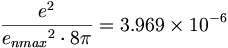$\frac{e^2}{{e_{nmax}}^2\cdot 8\pi}=3.969\times 10^{-6}$ (10.3)

各onnにはそれ自身の強い電荷があるので、それ自身の「弱い相互作用」定数をも持つだろう。陽子と中性子の微細構造定数としてpとnをそれぞれ指定し、記すことができるのは：

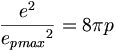$\frac{e^2}{{e_{pmax}}^2}=8\pi p$ (10.4) 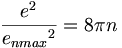$\frac{e^2}{{e_{nmax}}^2}=8\pi n$ (10.5)

方程式10.1、10.4、および10.5は、各onnのために統一電荷方程式を表す。共に取られた、これらの方程式は力の統一理論のための基礎である。

電荷の幾何学

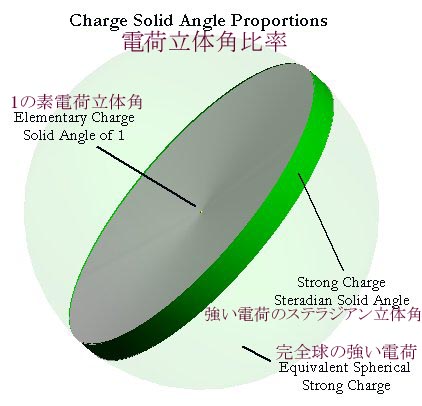
統一電荷方程式はontaのための一般的な幾何学を決定付ける。電荷幾何学の概念が新しいので、我々は球形の静電荷の幾何学がどうステラジアンと強い電荷の幾何学に変わるかを説明するつもりである。

図4は電子の2つの電荷を示す。静電荷は、1（明るい緑色の球の中心にある小さい黄色の球）の立体角を持ち、一方、強い電荷はステラジアンの立体角（深緑色のオビとして描かれる）を持つ。図形は、立体角を概念化しただけであり、単電子の形態は表現していない。

図 4

図 5

強い電荷が持つ立体角は球形の静電荷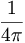 $\frac{1}{4\pi}$ に等しい。静電荷は球形のエーテル共振との幾何学的な関係に相当する1スピンを持つ。強い電荷はonn（亜原子粒子）角運動量の1/2スピンに相当する1/2スピンを持つ。それ故に、1/2スピンに2を掛けて1/2スピンを1スピンへ変換する。強い電荷のステラジアン立体角に4を掛けることで、強い電荷のステラジアン立体角を立体角球へ変換する。それゆえ、静電荷から強い電荷に関連する幾何学的な定数は以下に等しい：

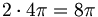$2\cdot 4\pi=8\pi$ (10.6)

電子の形は量子エーテル・ユニットのスピン位置の形に従う。

図 6

エーテルは5次元の空間共鳴をしており、電子の形が図5の航程線のように現れてくる。しかしながら、我々の人間の知覚力が線型時間に沿って動くので、時間-空間の4次元的な観点が適用される。それゆえに、物理的に具現化した人間にとっては、電子は図形6のような半スピン物質から作られた心臓形として、現れる。

力の法則

3つの認識された力として、重力定数、静電気、そして、強い力がある。弱い相互作用は力では全くなく、静電気と強い力の単なる割合である。重力は、強い電荷に対する一般的な質量の比率によって、強い力に正比例している。

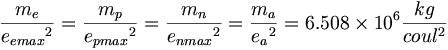$\frac{m_e}{{e_{emax}}^2}=\frac{m_p}{{e_{pmax}}^2}=\frac{m_n}{{e_{nmax}}^2}=\frac{m_a}{{e_{a}}^2}=6.508\times 10^6\frac{kg}{coul^2}$ (11.1)

重力に基づいて不正確に打ち立てられたアルバート・アインシュタインの一般相対性理論は、強い電荷に対する質量の一般的な比率に起因しており、それは静電荷と強い電荷の間の相互作用に基づくべきである。静電荷、弱い相互作用、および強い力はすべて共に動作する。静電荷についての静電気の力の法則は、非常に近い距離で利くのではなく、比較的長い距離で働く。さらに、強い電荷の法則は、超近接距離で電磁荷に関して有効であるが、比較的長距離に対しては有効ではない。帯電体の間の距離によっては、その2つの力は実際に入れ替わる。一般相対性理論は統一電荷方程式に基づいて展開するべきであった。陽子に関する例では、一般化されたアインシュタインの場の方程式と共に電荷方程式は以下のように記述される：

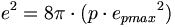$e^2=8\pi\cdot (p\cdot {e_{pmax}}^2)$ (11.2)

G = 8π T

(11.3)

静電力の法則（クーロンの法則）

クーロン法は静電荷間の力を支配する法則である。ねじり秤を使ったクーロンの実験は、静電位を最大にするために球面に取り組んだ。クーロンは、距離の二乗の逆数が静電荷量に比例していると主張した（数人の科学者き、彼が実際にこれ⁴⁵を観測したかどうかと疑っているが）：

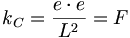$k_C=\frac{e\cdot e}{L^2}=F$ (11.4)

表現11.4には、クーロンの静電気定数があり、静電荷を意味している。ただし、Lは電荷間の距離で、Fは合力である。クーロンは、電荷が互いに非常に近くなる場合は、上記の法則には拘束されないことを観測した。これは強い電荷が支配し始めるからである。しかしながら、静電荷支配と電磁荷支配の間の境界はゆるやかである。我々は、これら2つの力の間のバランスが、弱い相互作用になると仮定する。

重力の法則

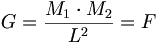$G=\frac{M_1\cdot M_2}{L^2}=F$ (11.5)

アイザック・ニュートン卿は式11.5のような重力定数の法を打ち立てた。Gはニュートンの重力定数で、M1とM2は2つの質量であり、Lは質量間の距離であり、そして、Fは質量間の力である。重力の初期の研究では、Henry CavendishがG⁴⁷の値を大変正確に測定した。重力法則の本質に関して考えるときに情報は広く利用可能であり、したがって、ここでは詳しく触れない。

強い力の法則

強い力の法則は、この論文以前は、現代物理学には知られていなかった。確立した物理学理論によると、強い力は「物理学では、原子核の中で基本粒子群を互いに結合する力、および、基本粒子の中でクォーク同士を互いに結合する力」⁴⁸ということである。パイ・メソンとグルオンが実際的には強い力の担体ではないために、過去に確立した物理学における強い力について計算するための実用的な方程式がない。しかしながら強い力は、電磁荷、または強い電荷を使用することでエーテル物理学モデルで計算される。強い力の法則は、静電力の法則と重力の法則の構造と同様である。静電気の法則の場合では、2つの強い電荷の積は、それぞれの電荷というただ一つの次元から計算する。陽子と中性子の拘束力は大きい「小半径」と小さい「大半径」を持つためなので、そのontaは球体として顕れる。したがって、クーロン定数はエーテル・ユニット定数の代わりの力の媒介である。

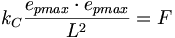$k_C\frac{e_{pmax}\cdot e_{pmax}}{L^2}=F$ (11.6)

中性子の強い力も同様に計算される：

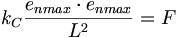$k_C\frac{e_{nmax}\cdot e_{nmax}}{L^2}=F$ (11.7)

結合していない自由な陽子と自由な中性子のための強い力の法則は、エーテル・ユニット定数を使用することで始まりそうであるが、クーロン定数は一回だけonta拘束に使用すると目測される。結合していない自由な陽子と自由な中性子のほうが形においてよりトロイダル状であるので、拘束されたontaは形において球体⁴⁹なのである。エーテルは、別のonnがあるかどうかに関わらず、いつも強い電荷に作用しており、1onnあたりの強い力は、実際に単一のonnの強い力である。言い換えれば、力と相互作用する他のどんなonnさえも周囲にないときさえ、エーテルは力を発生する為にontaに作用している。ontaには、別のonnが近くにある事を感知しそれに反応することができるような近接場システムがないからであるに違いない。原子核の総核拘束力は、一つの原子核の中のontaに作用するすべての力の合計である。どんな他の中性子も陽子も近くにない単一の中性子に作用する力の合計は：

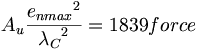$A_u\frac{{e_{nmax}}^2}{{\lambda_C}^2}=1839force$ (11.8)

しかしながら、拘束されている間のonta半径の変化に応じた、一つの重水素の原子核の強い力の総合計は以下の通りである：

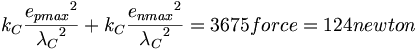$k_C\frac{{e_{pmax}}^2}{{\lambda_C}^2}+k_C\frac{{e_{nmax}}^2}{{\lambda_C}^2}=3675force=124newton$ (11.9)

その原子核の強い力の表現は以下の通りである：

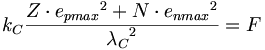$k_C\frac{Z\cdot {e_{pmax}}^2+N\cdot {e_{nmax}}^2}{{\lambda_C}^2}=F$ (11.10)

ここで、Zは陽子の数であり、Nはその原子核の中の中性子の数である。原子核の強い力の方程式は核の拘束力を定量化する。すべての同位元素の原子核の結合エネルギーを予測する原子核結合エネルギー方程式は、まだ完全ではないが完成しつつある。

力の担体の相対的強さ

エーテル物理学モデルでは、力の担体は、静電荷と、電磁荷と、質量である。いわゆる「弱い力」は電磁荷に対する静電荷の割合である。単一次元電荷としての力の相対的強度を決定する確立された単位システムで実験というものが言い表わされるので、我々は相対的な強さを観測するためにAPM電荷の平方根と単一次元電荷を比較しなければならないだろう。静電荷に関しては、陽子と中性子の強い電荷は、それぞれ大きさにおいて100倍近く大きい。電子の強い電荷は静電荷より2.335倍強いだけである。確立した物理学は電子の強い電荷を認識していない。

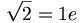$\sqrt{2}=1e$ (11.11) 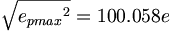$\sqrt{{e_{pmax}}^2}=100.058e$ (11.12) 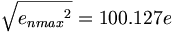$\sqrt{{e_{nmax}}^2}=100.127e$ (11.13) 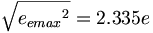$\sqrt{{e_{emax}}^2}=2.335e$ (11.14)

力の担体の相対的な強さ

表 2

	力の統一理論相対的な電荷の強さ	確立された相対的力の担体の強さ
素電荷	1	1
強い電荷
陽子	100.058	100
中性子	100.127	100
電子	2.335	(認識されていない電子の強い核力)
弱い相互作用
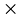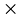陽子	9.988 $\times$ 10^-5	10 $\times$ 10^-5
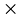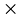中性子	9.975 $\times$ 10^-5	10 $\times$ 10^-5
電子	0.183	(認識されていない電子の弱い相互作用)

陽子と中性子の弱い核相互作用は、以下のように計算する：

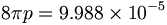$8\pi p=9.988\times 10^{-5}$ (11.15) 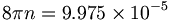$8\pi n=9.975\times 10^{-5}$ (11.16)

両方の結果が既に静電荷を強い電荷と比較する比率であるので、それらはただそのようになっている。

その他

エーテルの秘密Secrets of the Aether (http://www.16pi2.com/book.htm)に示されるようにエーテル物理学モデルの多くの拡張版がある。以下は、開発された概念サンプルである。我々は核と電子の拘束力方程式、真に量子化された光子、対生成、ベータ崩壊、渦電流、核の構造、ゼロ点エネルギー、なぜ物体総量が現在の形を取るようになったかの定量化、陽子と電子の質量の定量化の可能性、意識、複雑さ(分類学に密接に関連する)の科学、および他の多くのテーマの方程式も打ち立てる。

中性子の定量化

中性子は拘束された電子と陽子として定量化される。エーテルが、電子と陽子が同じスピン位置を相互に共有するようにして包む。

図 7

陽子と電子の間で形成される空洞は、エーテル・ユニットの間に存在する暗黒物質をカプセル状に包む。この閉じ込められた暗黒物質はニュートリノになる。反ニュートリノが閉じ込められた空洞は、本質的に電磁気であるが、電子と陽子が拘束された強い電荷である。したがって、その空洞は、スピン位置と強い電荷の幾何学的規則に従わなければならず、それは、すべての量子幾何学がそうであるように、半径という単位で説明される。もしそれがエーテル構造の中に存在しているならば、ニュートリノの幾何学はトロイダル状(4π²)であるに違いない。そのうえ、反ニュートリノが電子と結合するので、電子と陽子エーテル・ユニットマイナス半スピンの半分の位置に存在している。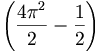 $\left (\frac{4\pi^2}{2}-\frac{1}{2}\right )$ 付加すれば、反ニュートリノが強い電荷で拘束されている陽子と電子の間に存在しているので、【ニュートリノは】ステラジアン角度を持たなければならない。これは以下として対電子角運動量と言われる反ニュートリノ角運動量を以下のように与える：

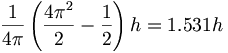$\frac{1}{4\pi}\left (\frac{4\pi^2}{2}-\frac{1}{2}\right )h=1.531h$ (12.1)

簡略化すると、以下を得る：

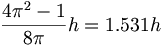$\frac{4\pi^2-1}{8\pi}h=1.531h$ (12.2)

方程式12.2は、ベータ崩壊の間に解放されたニュートリノの観測された挙動を反映する。確立された物理学では、このニュートリノを「反ニュートリノ」として名づける。しかしながら、そのニュートリノが陽子と電子に同じスピン方向を共有しなければならないので、我々はそれを正しくニュートリノと名付けるだろう。反ニュートリノは拘束された陽電子と反陽子の間に存在しているだろう。ベータ崩壊が「弱い相互作用」に起因するので、ニュートリノはパリティ保存則に違反することができる。これを理解するために、我々は、静電気拘束からのスピンが2ontaそして、ミラーに起因することを観測する。強い電荷拘束からのスピンは2つのontaとミラーのためである。しかしながら、崩壊プロセスにおけるニュートリノに起因するスピンはニュートリノだけが関与し、したがって、1つのスピンパリティしかない。また、我々が方程式12.2で観測するのは、8πが弱い相互作用定数であることである。

中性子磁気モーメント

磁気モーメントはonnの強い電荷に対してエーテルの静電荷の影響を測定する単位である。SI単位におけるNIST⁵⁰によって定義された電子の磁気モーメントは以下の通りである：

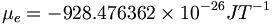$\mu_e=-928.476362\times 10^{-26}JT^{-1}$ (12.3)

電子の磁気モーメントのNIST値は、量子測定系では次のように表わされる：

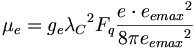$\mu_e=g_e{\lambda_C}^2F_q\frac{e\cdot {e_{emax}}^2}{8\pi{e_{emax}}^2}$ (12.4)

ここで、ラム・シフト系で測定された電子のg-ファクターがある。磁気モーメントの電子単位で、強い電荷は相殺する。なぜなら、電子は電子に対して作用するから。それにもかかわらず、方程式には強い電荷項が、他の測定系の磁気モーメント値ontaに対して電子が作用しているのを示すためにある。g-ファクターはontaの磁気モーメントに関連する不可欠の値である。onnの歳差運動を修正するために。SI単位における陽子磁気モーメントのNIST値⁵⁰は以下の通りである。

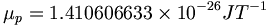$\mu_p=1.410606633\times 10^{-26}JT^{-1}$ (12.5)

陽子磁気モーメントのNIST値は、量子測定系の中で以下のように表わされる。

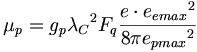$\mu_p=g_p{\lambda_C}^2F_q\frac{e\cdot {e_{emax}}^2}{8\pi{e_{pmax}}^2}$ (12.6)

ここで、陽子のg-ファクターは、NISTに関してリストされた5.58569である。中性子磁気モーメントのNIST値⁵⁰は、SI単位系では以下のように表わされる。

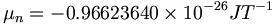$\mu_n=-0.96623640\times 10^{-26}JT^{-1}$ (12.7)

そして、以下のように量子測定値で表すことができる：

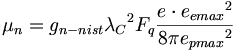$\mu_n=g_{n-nist}{\lambda_C}^2F_q\frac{e\cdot {e_{emax}}^2}{8\pi{e_{pmax}}^2}$ (12.8)

ここで $g n-nist$ は、中性子のg-ファクターで、NIST⁵⁰によって定義される-3.82608545である。方程式が中性子の代わりに陽子の強い電荷を使用することでバランスをとっている点に注意。これは非常にありそうもない。中性子の磁気モーメントデータが読み違いであったか、または、中性子のg-ファクター値が単に誤算されたように見える。中性子磁気モーメントは陽子の強い電荷に依存し、そして、そのような訳で、陽子の質量に関して、不可能に見える。上記の分析では、すべての電荷は素電荷を含めて、分配されるべきであると、かなり断定的に示してもいる。Charles Coulombの観測に基づき、全ての電荷は、活動の力の法則のために分配されなければならない。そして、エーテル物理学モデルの一貫性のために、我々は磁気モーメント静電荷次元を転移させる。APMシステムの電子磁気モーメントは以下の通りである：

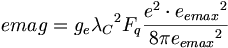$emag=g_e{\lambda_C}^2F_q\frac{e^2\cdot {e_{emax}}^2}{8\pi{e_{emax}}^2}$ (12.9)

APMシステムの陽子磁気モーメントは以下の通りである：

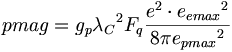$pmag=g_p{\lambda_C}^2F_q\frac{e^2\cdot {e_{emax}}^2}{8\pi{e_{pmax}}^2}$ (12.10)

そして、中性子磁気モーメントのためにNIST値に基づくと、その中性子磁気モーメントは次のようになるだろう：

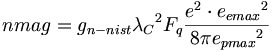$nmag=g_{n-nist}{\lambda_C}^2F_q\frac{e^2\cdot {e_{emax}}^2}{8\pi{e_{pmax}}^2}$ (12.11)

しかしながら、自然が、陽子の強い電荷に起因する磁気モーメントを中性子に与えることは、非常にありそうもないことである。したがって、磁気モーメントの精度を仮定して、量子測定値を修正すると、中性子のg-ファクターが変化する：

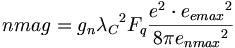$nmag=g_n{\lambda_C}^2F_q\frac{e^2\cdot {e_{emax}}^2}{8\pi{e_{nmax}}^2}$ (12.12)

測定が正確であるならば、中性子のg-ファクター( $g n$ )は-3.831359であるに違いない。これは-3.826085のNIST中性子g-ファクター( $g n-nist$ )と比較される。エーテル物理学モデルにおける磁気モーメントの表現から、各onnの中で静電荷と電磁荷の相互作用によって物理学的に磁気モーメントが顕現してくる。さらに明らかなのは、電子が、それぞれのontaの磁気モーメントを引き起こす際に重要な役割を果たすことである。

g-ファクター

図 8

図8で、三角形の辺bは単位長であり、心臓形曲線がかかる球の半径に等しい。そこに見られるように、辺aは単位長の半分であり、辺cは直角三角形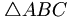 $\triangle ABC$ の斜辺である。そして、 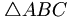$\triangle ABC$ は直角三角形の特別な形であり、ここで辺bは辺aの2倍でありファイ三角形（黄金比三角形ではない）と呼ぶ事が出来る。ファイ三角形がそのように命名されたのは、b=1の単位三角形では、

$c + a = Phi$ (12.13)

そして

$c - a = phi$ (12.14)

ここで、 Phi は黄金比であり、phi がその逆数である。これは単位長bに関してピタゴラスの表現cとaを代わりに用いることによって、容易に立証される：

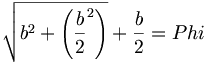$\sqrt{b^2+ \left ({\frac{b}{2}}^2\right )}+\frac{b}{2}=Phi$ (12.15)

b=1故に、我々は以下を得る：

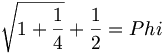$\sqrt{1+ \frac{1}{4}}+\frac{1}{2}=Phi$ (12.16)

$1.118 + .5 = 1.618 = Phi$ (12.17)

以下のように、値phiは同様に減少する：

$1.118 - .5 = 0.618 = phi$ (12.18)

亜原子はそれらの角運動量であるので、g-ファクターがエーテル・ユニットを通してスピンしながらの螺旋LC(ligamen circulatus)と等しく、以下のように定量化される：

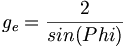$g_e=\frac{2}{sin(Phi)}$ (12.19)

陽子g-ファクターは以下のように定量化される：

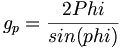$g_p=\frac{2Phi}{sin(phi)}$ (12.20)

中性子の定量化で示されるように、それは陽子に電子が拘束された複合粒子である。中性子g-ファクターの解決法は以下の通りである：

$g_n=2sin(1)\frac{sin(phi)}{\left [Phi\left (-sin(Phi)+sin(Phi)\cdot cos(Phi)^2+sin(1)-sin(1)\cdot cos(Phi)^2\right ) \right ]}$ (12.21)

これは確立した物理学の測定値と観察⁵¹に一致している。しかしながら、注意して欲しいのは、APMで計算された電子と陽子のg-ファクターは、現代物理学が十分に大きな値で正確に推定するために、その電子と陽子のg-ファクターの1000分の1に合致するだけであることを。付加するに、電子のg-ファクターが負の値によって定量化されるのは、電子の陰電荷の特性であると推定される。しかしながら、中性子g-ファクターにもまた、負の値がある。中性子に中性の電荷があるとしたときに、同じ論理は電子と中性子の両方に適用することができるか？その論理では電子の負のg-ファクターを裏づけない。この理由で、電子のg-ファクターは正の値をAPMでは持っている。

結論

エーテル物理学モデルは、数学的に存続可能であり、現代物理学と同様の実証的なデータに基礎を持つ。我々はここにAPMのほんの一部分だけを提示するが、当理論を科学界が精査するために、そして、確認するかまたは論駁する為の充分な事例がある。力の統一理論の約束は十分な動機であるが、また、当モデルは、量子レベルから宇宙レベルまでの宇宙の本質に関するずっと多くの答えられていない質問に答えるものであると提議する。

APMには、科学のすべてを一つの広大な理論に統合させる可能性がある。その結果、すべてのものを説明する真の理論を提供する。他のどんな理論も、エーテル物理学モデル程に適用範囲と展望がほとんど合致したためしがない。

我々は、この論文の編集で我々を指導してくれたPhil Risby博士に特別な感謝を表したい。

参照

1. Sir Edmund Whittaker, A History of the Theories of Aether and Electricity; The Classical Theories (London; New York, American Institute of Physics, 1987) p. 6
2. Ibid pp. 95-96
3. The Ether, Science, Vol. 18, No. 447. (Aug. 28, 1891), pp. 119-122.
4. Lawrence M. Cockaday, New York Herald Tribune, (Sept. 22, 1929), pp. 1, 29.
5. Dayton C. Miller, Science, New Series, Vol. 63, No. 1635 (Apr. 30, 1926), pp. 433-443
6. “The outcome of the Michelson - Morley experiment would, therefore, suggest that the ether is dragged along with the earth, as far as the immediate neighborhood of the earth is concerned.” Peter Gabriel Bergmann, Introduction to the Theory of Relativity (New York, Prentice Hall Inc., 1947) p. 27
7. Quoted from Abraham Pais, Subtle Is the Lord: The Science and the Life of Albert Einstein (Oxford: Oxford University Press, 1982) p. 113.
8. Albert P. Carman, Science, New Series, Vol. 71, No. 1834 (Feb. 21, 1930), pp. 214-215.
9. Robert Matthews, Science, New Series, Vol. 263, No. 5147. (Feb. 4, 1994), pp. 612-613
10. John D. Norton, General Covariance and the Foundations of General Relativity: Eight Decades of Dispute, Rep. Prog. Phys. 56 (1993) pp. 791-858 printed in UK.
11. Michel Janssen et al, The Collected Papers of Albert Einstein Vol. 7, The Berlin Years: Writings , 1918 ? 1921 (Princeton University Press, 2002) pp. 305?309; 321
12. Robert S. Shankland, Science, New Series, Vol. 176, No. 4035 (May 12, 1972), pp. 652-653
13. David W. Thomson and Jim D. Bourassa, Secrets of the Aether; Second Edition (Alma, IL, The Aenor Trust, 2005)
14. Ibid Secrets of the Aether, p 97
15. Ibid Secrets of the Aether, p 17
16. Ibid Secrets of the Aether, p 38
17. "Above all, Coulomb confirmed by very refined methods the fact already noticed by Gray, that electricity is only situated on the external surface of conductors; and he observed that this also is a consequence of the inverse square law, and can only be true if the latter holds exactly." Philipp Lenard, Great Men of Science: A History of Scientific Progress, trans. H. Stafford Hatfield (New York: The Macmillan Company, 1933) pp. 157-8.
18. Max Planck, Where Is Science Going?, trans. James Murphy, 1st ed. (New York: Norton, 1932) 59.
19. Ibid Secrets of the Aether, pp 15, 34, 36
20. G. W. Ludwig, Science, New Series, Vol. 135, No. 3507. (Mar. 16, 1962), pp. 899-905.
21. Arthur L. Robinson, Science, New Series, Vol. 217, No. 4565. (Sep. 17, 1982), pp. 1127-1129.
22. Ibid Secrets of the Aether, pp. 41-51
23. Arthur L. Robinson, Science, New Series, Vol. 222, No. 4630. (Dec. 23, 1983), pp. 1316-1317.
24. Ibid Secrets of the Aether, p. 62
25. NIST Reference on Constants, Units, and Uncertainty (http://physics.nist.gov/cgi-bin/cuu/Value?me|search_for=electron+mass)
26. NIST Reference on Constants, Units, and Uncertainty (http://physics.nist.gov/cgi-bin/cuu/Value?mp|search_for=proton+mass)
27. NIST Reference on Constants, Units, and Uncertainty (http://physics.nist.gov/cgi-bin/cuu/Value?mn|search_for=neutron+mass)
28. Ibid Secrets of the Aether, p. 50
29. NIST Reference on Constants, Units, and Uncertainty (http://physics.nist.gov/cgi-bin/cuu/Value?e|search_for=elementary+charge)
30. NIST Reference on Constants, Units, and Uncertainty (http://physics.nist.gov/cgi-bin/cuu/Value?ecomwl|search_for=compton+wavelength)
31. Ibid Secrets of the Aether, p. 33
32. Ibid Secrets of the Aether, p. 33
33. Ibid Secrets of the Aether, p. 38
34. Ibid Secrets of the Aether, pp. 103, 131
35. Ibid Secrets of the Aether, pp. 130-132
36. Ibid Secrets of the Aether, p. 33
37. C. N. Yang, Science, New Series, Vol. 127, No. 3298, (Mar. 14, 1958), pp. 565-569
38. Hannes Alfven. Worlds-Antiworlds: Antimatter in Cosmology (W H Freeman & Co, 1966) ISBN: 0716703173
39. Ibid Secrets of the Aether, pp. 164-168
40. Ibid Secrets of the Aether, pp. 171-173
41. Max Planck, Where Is Science Going?, trans. James Murphy, 1st ed. (New York: Norton, 1932) p. 59.
42. Henry Margenau, Open Vistas Philosophical Perspectives of Modern Science (New Haven, CT: Yale University Press, 1961) p. 118.
43. Charles Seife, Science, New Series, Vol. 275, No. 5297. (Jan. 10, 1997), p. 158.
44. Lamoreaux, Steven K., Demonstration of the Casimir Force in the 0.6 to 6 mm Range (Phys Rev Let, Vol 78, Num 1, 1996)
45. Steven Dickman, Science, New Series, Vol. 262, No. 5133. (Oct. 22, 1993), pp. 500-501
46. Quoting the writings of Charles Coulomb. Morris H. Shamos, Great Experiments in Physics: Firsthand Accounts from Galileo to Einstein (Dover Publications Inc., New York, reprint 1987) p. 65
47. "Gravitation ," The Columbia Encyclopedia , 6th ed.
48. The New Dictionary of Cultural Literacy, Third Edition Edited by E.D. Hirsch, et al.
49. Ibid Secrets of the Aether, p. 33
50. National Institute of Standards and Technology, The NIST Reference on Constants, Units, and Uncertainty (http://physics.nist.gov/cuu/Constants/index.html)
51. F. J. Belinfante, Science, New Series, Vol. 118, No. 3067. (Oct. 9, 1953), p. 397.

論文： 物理学のための新しい基礎, by 量子エーテル力学研究所